PDF Archives - Page 7 of 20 - Master Every Task with Clear Guidelines

Bybeatrice

parent functions chart pdf

Parent functions are foundational functions in mathematics, serving as the basis for understanding more complex transformations. A parent functions chart provides a visual reference for comparing graphs and properties, such as domain, range, and end behavior, enabling structured analysis of function transformations and their applications.

1.1 Definition and Importance of Parent Functions

Parent functions are basic function forms that serve as building blocks for more complex functions. They are essential for understanding function transformations, as they provide a reference point for identifying and analyzing changes. The parent functions chart organizes these foundational functions, highlighting their unique characteristics, such as domain, range, and end behavior, which are critical for solving problems and modeling real-world applications.

1;2 Overview of the Parent Functions Chart

The parent functions chart is a visual tool that categorizes and compares basic functions, such as linear, quadratic, and square root functions. It displays their graphs, equations, and key attributes like domain, range, and end behavior. This chart helps students identify patterns and understand how transformations alter graphs, making it an essential resource for analyzing and sketching functions effectively.

Types of Parent Functions

Parent functions include linear, quadratic, cubic, absolute value, piecewise, root, and rational functions, each with unique graphs and properties, forming the basis for more complex function transformations.

2.1 Linear Functions

Linear functions are represented by equations of the form f(x) = mx + b. They have straight-line graphs with a constant slope (m) and y-intercept (b). These functions are essential in modeling real-world phenomena like constant rates of change. Their graphs exhibit Odd symmetry and have a domain and range of all real numbers, making them foundational for understanding more complex function behaviors.

2.2 Nonlinear Functions (Quadratic, Cubic, etc.)

Nonlinear functions, such as quadratic (f(x) = ax² + bx + c) and cubic (f(x) = ax³ + bx² + cx + d), exhibit curved graphs. Quadratic functions form parabolas, while cubic functions have an “S” shape with one inflection point. These functions are crucial for modeling real-world phenomena like growth rates and energy consumption, differing from linear functions in their non-constant rates of change and complex graph behaviors.

2.3 Absolute Value and Piecewise Functions

Absolute value functions, like f(x) = |x|, create a V-shaped graph with a vertex at the origin, while piecewise functions combine multiple functions over specific intervals. These functions are essential for modeling real-world scenarios requiring conditional behavior, such as distance calculations or stepwise processes, and are often analyzed using parent function charts for their unique graphing and transformational properties.

2.4 Root and Rational Functions

Root functions, such as f(x) = √x and f(x) = ∛x, involve radicals and have restricted domains and ranges. Rational functions, like f(x) = 1/x, are ratios of polynomials, often featuring asymptotes and points of discontinuity. The parent functions chart helps visualize these functions, highlighting their unique characteristics and behaviors, which are essential for modeling real-world phenomena and solving complex problems.

Graphical Transformations of Parent Functions

Graphical transformations include vertical shifts, horizontal shifts, stretching, compressing, and reflections. These transformations alter the parent function’s graph, enabling the analysis of how functions change in shape and position.

3.1 Vertical and Horizontal Shifts

Vertical shifts move a graph up or down by adding or subtracting a constant to the function. Horizontal shifts move the graph left or right by adding or subtracting a constant inside the function; These transformations are essential for modifying parent functions to create new functions, as shown in the parent functions chart. Examples include f(x) + c for vertical shifts and f(x ⸺ h) for horizontal shifts.

3.2 Stretching and Compressing (Scaling)

Scaling involves stretching or compressing a function vertically or horizontally. Vertical scaling multiplies the function by a constant a, stretching it if a > 1 or compressing it if 0 < a < 1. Horizontal scaling applies a factor 1/a inside the function, affecting the x-axis. This transformation alters the graph's appearance without changing its basic shape or orientation, as detailed in the parent functions chart.

3.3 Reflections Over the x-axis or y-axis

Reflections flip a function over the x-axis or y-axis. Reflecting over the x-axis multiplies the function by -1, flipping it vertically. Reflecting over the y-axis replaces x with -x, mirroring the graph horizontally. These transformations change the direction of the graph but not its basic shape or orientation, as illustrated in the parent functions chart for visual understanding and analysis.

3.4 Combining Multiple Transformations

Combining transformations involves applying multiple changes to a parent function, such as shifts, reflections, and scaling. The order of transformations matters, as vertical shifts occur before horizontal ones, and scaling can precede or follow depending on the function. The parent functions chart helps visualize these combinations, enabling clear identification of how transformations alter the graph’s appearance and behavior systematically.

Attributes of Parent Functions

Essential attributes include domain, range, end behavior, symmetry, and intervals. These properties help analyze functions, with the chart organizing traits for easy comparison and study.

4.1 Domain and Range

The domain of a function describes all possible input values (x-values), while the range describes all possible output values (y-values). Understanding these attributes is crucial for analyzing function behavior and transformations. The parent functions chart provides a clear visual representation of these attributes, making it easier to identify and compare domain and range across different functions. This helps in understanding their behavior and limitations.

4.2 End Behavior and Symmetry

End behavior describes how a function behaves as ( x ) approaches infinity or negative infinity, providing insights into its long-term trends. Symmetry refers to whether a function is odd, even, or neither, determined by its behavior around the y-axis or origin. The parent functions chart highlights these properties, aiding in the identification and comparison of function symmetry and end behavior patterns.

4.3 Increasing or Decreasing Intervals

The parent functions chart helps identify intervals where functions are increasing or decreasing. For example, linear functions have consistent behavior, while absolute value functions change direction at their vertex. Understanding these intervals is crucial for analyzing function transformations and predicting behavior, making the chart an essential tool for visualizing and comparing function growth patterns effectively.

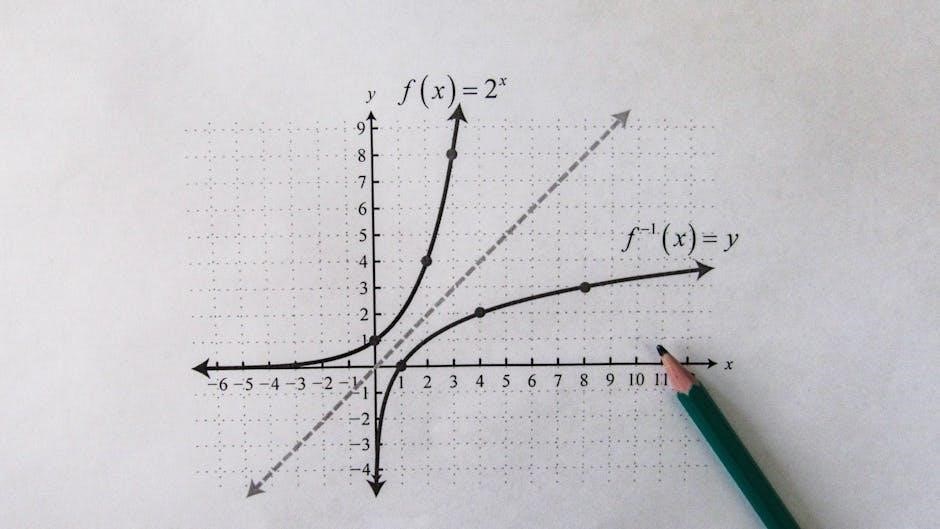
Using the Parent Functions Chart

The parent functions chart is a visual tool for identifying basic functions and analyzing their transformations. It helps sketch graphs, understand domain/range, and predict end behavior effectively.

5.1 Identifying Basic Functions

The parent functions chart is a visual guide for identifying basic functions, such as linear, quadratic, cubic, and absolute value functions. It provides graphs, equations, and key characteristics, enabling quick recognition and comparison. By referencing the chart, users can easily identify the parent function for any transformed function, aiding in sketching and analyzing graphs effectively.

5.2 Analyzing Transformations

Using the parent functions chart, transformations can be analyzed by comparing the original function to its transformed version. Vertical shifts, horizontal shifts, stretches, compressions, and reflections can be identified by noting changes in the equation or graph. This process aids in determining the specific transformation applied to the parent function, enhancing understanding of function behavior and relationships.

5.3 Sketching Graphs

Sketching graphs using the parent functions chart involves identifying the basic function and applying transformations. Start with the parent function, then systematically apply vertical/horizontal shifts, stretches, or reflections. Key points like intercepts, vertices, and asymptotes guide the sketch. This method ensures accuracy and helps visualize how transformations alter the original graph’s shape and position, aiding in understanding function behavior.

Examples and Applications

Parent functions model real-world phenomena, such as linear growth in economics and quadratic paths in physics. Transformations solve practical problems, demonstrating the chart’s versatility in real applications.

6.1 Real-World Applications of Parent Functions

Parent functions are essential in modeling real-world scenarios. For instance, linear functions describe population growth rates, while quadratic functions model projectile motion in physics. The parent functions chart pdf provides clear visual aids to understand these applications, making complex problems more approachable. These functions are also used in economics, engineering, and environmental science to predict trends and behavior.

6.2 Solving Problems with Transformations

Understanding transformations of parent functions is crucial for solving real-world problems. By analyzing shifts, stretches, and reflections, students can model scenarios like sound waves or financial trends. The parent functions chart pdf aids in identifying these transformations, enabling learners to predict outcomes and solve complex equations systematically. This skill enhances problem-solving abilities in math and science.

Educational Resources

Utilize PDF guides and online tools like Khan Academy for detailed explanations of parent functions. SMART Technologies offers interactive resources for visual learning and practice exercises.

7.1 PDF Guides and Worksheets

PDF guides and worksheets are essential resources for mastering parent functions. They often include detailed charts, examples, and exercises to practice identifying and graphing functions. These resources are structured to cover basic concepts and complex transformations, making them ideal for self-study or classroom use. Educators and students rely on them to reinforce learning and prepare for assessments;

Many PDFs, such as those from SMART Technologies, provide interactive elements and visual aids. Worksheets focus on specific skills like domain/range identification and function analysis, offering a hands-on approach to understanding parent functions and their applications.

7.2 Online Tools and Tutorials

Online tools and tutorials offer interactive ways to explore parent functions. Websites like Khan Academy provide video lessons and exercises for understanding function transformations. Interactive graphing tools allow users to visualize changes to parent functions in real-time. These resources are ideal for self-paced learning, making complex concepts like domain, range, and symmetry more accessible and engaging for students.

Best Practices for Learning Parent Functions

Use a parent functions chart as a visual guide to compare function types. Regularly practice graphing and identifying transformations. Review common mistakes to strengthen understanding and retention of key concepts.

8.1 Structured Study Techniques

Use the parent functions chart as a visual learning tool. Create flashcards for each function type. Practice categorizing functions by their graphs and equations. Regularly review transformations and their effects. Focus on identifying patterns and relationships. Track common mistakes to avoid them. Prioritize understanding over memorization. Incorporate real-world applications to enhance retention. Schedule regular review sessions to reinforce concepts and build confidence.

8.2 Common Mistakes to Avoid

Common mistakes include confusing vertical and horizontal shifts, misidentifying domain and range restrictions, and incorrectly applying transformation scales. Students often mix up function types, such as quadratic and cubic behaviors. Additionally, neglecting to consider end behavior when analyzing transformations is a frequent error. Always double-check function characteristics and transformation rules to avoid these pitfalls and ensure accurate graphing and analysis.

Bybeatrice

thank you maam pdf

Thank You‚ Ma’am by Langston Hughes is a poignant short story exploring themes of kindness‚ redemption‚ and societal influences․ Published in 1958‚ it highlights a transformative encounter between a young boy and a compassionate woman‚ delving into moral growth and human connection․

Plot Summary

A young boy attempts to steal a woman’s purse‚ but she catches him and‚ instead of punishing‚ takes him home to teach morality and kindness․

Setting

The story unfolds in a city at night‚ specifically around 11 o’clock‚ creating a tense urban atmosphere․ The woman is walking alone when the boy attempts to steal her purse․ The setting emphasizes the isolation and vulnerability of the moment‚ contrasting with the warmth of the woman’s home‚ where she takes the boy to teach him a lesson․ This shift from a public to a private space highlights the transformation in their interaction‚ showcasing the woman’s kindness and the boy’s potential for change․ The urban setting also reflects the social and economic challenges of the time‚ adding depth to the narrative․

The Incident

The incident begins with a young boy attempting to steal Mrs․ Jones’s large‚ heavily laden purse․ The boy‚ driven by unknown motives‚ tries to snatch the purse as she walks alone at night․ However‚ the strap breaks‚ and he fails to escape․ Mrs․ Jones catches him and‚ instead of punishing him‚ decides to take him to her home․ She cleans him up‚ feeds him‚ and teaches him about right and wrong․ This pivotal moment shifts the narrative from a potential crime to an act of kindness‚ setting the stage for the boy’s moral awakening․ The incident highlights the woman’s compassion and her belief in the boy’s potential for redemption․

Major Characters

Mrs․ Luella Bates Washington Jones is a strong‚ compassionate woman who embodies kindness and wisdom․ Roger is a misguided boy whose encounter with her changes his perspective on life․ Their dynamic drives the story’s moral core․

Mrs․ Luella Bates Washington Jones

Mrs․ Jones is a central figure in the story‚ portrayed as a large‚ strong-willed woman with a deep sense of morality․ Her large purse‚ filled with various items‚ symbolizes her preparedness and resourcefulness․ When Roger attempts to steal her purse‚ her reaction is not one of anger but of understanding and compassion․ She chooses to teach him a lesson by inviting him into her home‚ showing him kindness‚ and offering him food․ Her actions reflect her belief in redemption and the importance of guiding others‚ especially the youth‚ toward the right path․ Through her character‚ Hughes highlights the transformative power of kindness and the impact one person can have on another’s life․ Mrs․ Jones’s decision to help Roger‚ rather than punish him‚ underscores her maternal instincts and her desire to see him become a better person․ Her approach to the situation is both firm and gentle‚ illustrating her wisdom and empathy․ Overall‚ Mrs․ Jones is a symbol of hope and the possibility of change in a challenging world․

Roger

Roger is a young boy who attempts to steal Mrs․ Jones’s purse‚ driven by a mix of desperation and naivety․ His actions are impulsive‚ stemming from a lack of guidance and perhaps a sense of hopelessness․ Despite his initial defiance‚ Roger is deeply affected by Mrs․ Jones’s unexpected kindness and firmness․ Her decision to take him into her home and teach him right from wrong marks a turning point for him․ Throughout the story‚ Roger’s character evolves from a misguided youth to someone who begins to understand the value of honesty and respect․ His interactions with Mrs․ Jones reveal both his vulnerability and his capacity for change‚ making him a complex and dynamic character in the narrative․

Themes

Kindness and Redemption: The story highlights how compassion and understanding can transform lives․ Social and Economic Factors: It explores how poverty and societal neglect shape behavior‚ emphasizing the need for empathy and intervention․

Kindness and Redemption

In Thank You‚ Ma’am‚ kindness and redemption are central themes․ Mrs․ Luella Bates Washington Jones‚ despite being robbed‚ chooses compassion over punishment․ She invites Roger into her home‚ feeds him‚ and teaches him moral lessons‚ showing that kindness can transform lives․ Her actions symbolize redemption‚ as she offers Roger a chance to change his ways․ The story illustrates how empathy and understanding can lead to personal growth‚ emphasizing that kindness is a powerful tool for positive change․ Through Mrs․ Jones’s unwavering compassion‚ Hughes highlights the human capacity for forgiveness and the impact one person can have on another’s life․

Social and Economic Factors

Social and economic factors play a significant role in shaping the characters and their actions in Thank You‚ Ma’am․ The story reflects the societal challenges faced by individuals‚ particularly marginalized communities‚ during the time of its writing․ Roger’s attempt to steal Mrs․ Jones’s purse suggests economic hardship and a lack of guidance‚ while Mrs․ Jones’s kindness and wisdom highlight her resilience and strength despite her own societal struggles․ The story underscores how socioeconomic conditions can influence behavior‚ yet also emphasizes the human capacity to rise above these challenges through compassion and understanding․ Hughes uses the characters to illustrate broader societal issues‚ offering a nuanced exploration of race‚ class‚ and the importance of community support․ The narrative serves as a commentary on the social and economic disparities of the era‚ while also celebrating the transformative power of kindness․

Symbolism

The purse and blue suede shoes in Thank You‚ Ma’am are symbolic of deeper themes․ The purse represents Mrs․ Jones’s life experiences and resilience‚ while the shoes symbolize Roger’s desire for material possessions‚ highlighting societal pressures and personal aspirations‚ driving the narrative’s moral and emotional depth․

The Purse

The purse in Thank You‚ Ma’am is a significant symbol‚ representing Mrs․ Jones’s resilience and resourcefulness․ Described as large with a long strap‚ it contains everything except “hammer and nails‚” emphasizing its practicality․ The purse is not just an accessory but a reflection of her life experiences․ When Roger attempts to steal it‚ the broken strap symbolizes the disruption of her routine‚ yet she retains control‚ showcasing her strength․ The purse also symbolizes her ability to carry burdens‚ both literal and metaphorical‚ highlighting her endurance and wisdom․ Through the purse‚ Hughes underscores themes of resilience and the weight of life’s challenges‚ making it a vivid and meaningful element in the story․

The Blue Suede Shoes

The blue suede shoes in Thank You‚ Ma’am symbolize Roger’s desire for material possessions and his misguided priorities․ They represent the allure of transient attractions that lead him to make poor choices․ Mrs․ Jones‚ recognizing the emptiness of such desires‚ uses the shoes as a teachable moment․ By not allowing Roger to keep them‚ she redirects his focus toward more meaningful values․ The shoes also highlight the societal pressures that influence Roger’s actions‚ emphasizing the struggle between right and wrong․ Through this symbol‚ Hughes critiques the superficiality of materialism and underscores the importance of moral guidance in overcoming such temptations․

Analysis

In Thank You‚ Ma’am‚ Mrs․ Jones’s intervention in Roger’s life underscores his moral development‚ highlighting themes of kindness‚ redemption‚ and the profound impact of human compassion․

Author’s Message

Langston Hughes conveys a powerful message about the transformative impact of kindness and understanding in Thank You‚ Ma’am․ Through Mrs․ Jones’s unwavering compassion‚ Hughes emphasizes the importance of empathy over punishment‚ highlighting how a moment of grace can redirect a life․ The story critiques societal norms by showing that true change often begins with human connection rather than judgment․ Hughes also underscores the idea that everyone deserves the chance to learn from their mistakes‚ challenging readers to reconsider their assumptions about others․ This narrative reflects Hughes’s broader themes of social justice and the resilience of the human spirit‚ encouraging readers to embrace compassion as a catalyst for positive change․

Critical Reception

Thank You‚ Ma’am has been widely praised for its nuanced exploration of human behavior and societal issues․ Critics highlight Langston Hughes’s ability to craft a simple yet profound narrative that resonates deeply with readers․ The story’s focus on kindness‚ empathy‚ and redemption is seen as a powerful commentary on the potential for positive change in individuals․ Many reviewers appreciate how Hughes subtly addresses race and class through the characters’ interactions‚ offering a timeless lesson on understanding and compassion․ The story’s accessibility and universal themes have made it a favorite in educational settings‚ with scholars noting its ability to provoke critical thinking about morality and societal expectations․ Overall‚ Thank You‚ Ma’am is celebrated as a masterful blend of social commentary and emotional depth․

Bybeatrice

krapp’s last tape pdf

Samuel Beckett’s Krapp’s Last Tape is a profound one-act play exploring memory, regret, and the passage of time through its aging protagonist, Krapp.

The play centers on Krapp’s ritual of recording and listening to tapes of his younger self, revealing a life of lost opportunities and existential despair.

Written in 1958, it is a masterclass in minimalist theater, using a single character and a tape recorder to convey deep emotional and philosophical complexity.

1.1 Overview of the Play

Krapp’s Last Tape is a one-act play by Samuel Beckett, set in a dimly lit, cluttered room known as Krapp’s den. The play revolves around Krapp, a 69-year-old man, who listens to recordings of his younger self on his birthday. Using a tape recorder, he reflects on past ambitions, lost love, and personal losses, revealing a life marked by regret and existential despair. The play’s minimalist style and focus on Krapp’s internal struggle create a poignant exploration of memory and time.

1.2 Historical Context and Background

Written in 1958, Krapp’s Last Tape reflects Samuel Beckett’s fascination with existential themes and memory. The play emerged during a period of minimalist theater experimentation, influenced by Beckett’s earlier works like Waiting for Godot. It premiered in 1958 at the Royal Court Theatre in London, directed by Donald McWhinnie, and has since become a landmark of modernist drama, exploring universal human struggles with aging and self-reflection.

Plot Summary of “Krapp’s Last Tape”

Krapp, an aging man, reflects on his life by listening to recordings of his younger self, grappling with lost love and the passage of time on his 69th birthday.

2.1 The Setting: Krapp’s Den

Krapp’s den is a dimly lit, cluttered room reflecting his isolated existence. A small table with drawers holds his tape recorder and tapes, central to the play’s action. The space is sparse, with rusty, worn clothing and a sense of decay, emphasizing Krapp’s detachment from the world and his fixation on the past. The den symbolizes his inner turmoil and the passage of time.

2.2 The Narrative Structure: Past and Present

The play intertwines Krapp’s present reality with his past through taped recordings. On his 69th birthday, Krapp revisits a tape from 39 years earlier, contrasting his youthful ambitions with his current despair. The tapes serve as a bridge between timelines, creating a dialogue between his past and present selves. This structure highlights the passage of time and the futility of Krapp’s attempts to reconcile his aspirations with his aging reality.

Themes in “Krapp’s Last Tape”

The play explores memory, regret, and the passage of time, highlighting Krapp’s existential struggle with loneliness, self-delusion, and the futility of human endeavor.

3.1 Memory and Regret

Krapp’s obsessive listening to his past recordings reveals a profound interplay between memory and regret. The tapes, spanning decades, capture his youthful ambitions and lost love, now tinged with remorse. Memory distorts reality, making past choices seem both foolish and poignant. Krapp’s ritual of revisiting these recordings underscores the human tendency to dwell on what could have been, while also highlighting the futility of trying to recapture lost time. This duality of nostalgia and pain defines his existential struggle.

3.2 The Passage of Time and Mortality

The passage of time is a central theme in Krapp’s Last Tape, as the aging protagonist confronts his mortality through decades of recorded reflections. Krapp’s annual ritual of recording and listening to tapes captures the relentless progression of time, revealing how moments of youth become distant memories. The play’s sparse, dimly lit setting and Krapp’s frail appearance underscore the inevitability of aging and death, making time both a measure of loss and a reminder of life’s transient nature.

3.3 Loneliness and Isolation

Krapp’s existence is defined by profound loneliness and isolation, confined to his cluttered den with only his recordings for companionship. His inability to connect with others is mirrored by his physical and emotional detachment, as he fixates on past memories rather than engaging with the present. The play’s stark, solitary setting underscores Krapp’s existential isolation, highlighting the human condition’s inherent loneliness and the futility of seeking meaning in a seemingly indifferent world.

Character Analysis: Krapp

Krapp is a complex, aging protagonist consumed by regret and self-pity, clinging to his past through recordings that reveal his emotional and psychological decay over time.

4.1 Psychological Profile of Krapp

Krapp is a deeply introspective and melancholic character, his mind a labyrinth of memories and self-loathing. His psychological state is marked by regret, isolation, and a narcissistic obsession with his past self. Through his tapes, he confronts his failures and lost loves, revealing a man trapped in a cycle of nostalgia and despair, unable to escape the weight of his choices.

4.2 Krapp’s Relationship with His Past Self

Krapp’s relationship with his past self is a mix of nostalgia and self-criticism, as he listens to tapes of his younger voice. The recordings reveal his ambitions, regrets, and lost love, creating a dialogue between his present and past selves. This interaction underscores his longing for connection and his disdain for the choices he made, highlighting the tension between who he was and who he has become.

Dramatic Structure and Style

Krapp’s Last Tape features a minimalist structure, with a single act and one character. The play’s style relies on the tape recorder as a narrative device, emphasizing Krapp’s isolation and introspection through monologue.

5.1 The Use of Monologue

The play relies heavily on monologue, with Krapp engaging in a deeply personal and introspective dialogue with his past self through taped recordings. This monologue structure isolates Krapp, emphasizing his solitude and inner turmoil. The tapes serve as a medium for self-reflection, allowing Krapp to confront his regrets and failed ambitions. Beckett’s use of monologue creates a raw, intimate connection between Krapp and the audience, heightening the emotional and psychological depth of the narrative.

5.2 The Role of the Tape Recorder

The tape recorder is a central element in Krapp’s Last Tape, serving as both a tool for self-reflection and a symbol of Krapp’s obsession with his past. It bridges the gap between his present and former self, allowing him to revisit memories and critique his younger ambitions. The mechanical nature of the tape recorder underscores the detachment and rigidity of Krapp’s introspection, while its limitations mirror the fragility of human memory and the passage of time.

Symbolism in the Play

The tape recorder symbolizes memory and the fragmented self, while Krapp’s den represents isolation. These elements underscore existential themes of time, loss, and the human condition.

6.1 The Significance of the Tape Recorder

The tape recorder in Krapp’s Last Tape is a potent symbol of memory, self-reflection, and the fragmented nature of identity. It allows Krapp to revisit his past, creating a dialogue between his younger and older selves. The tapes serve as a medium for introspection, highlighting themes of regret, the passage of time, and the futility of human endeavor. Through this device, Beckett underscores the tension between the concrete past and the uncertain present, amplifying the play’s existential depth.

6.2 The Symbolism of Krapp’s Den

Krapp’s den is a cluttered, dimly lit space that symbolizes his intellectual and emotional isolation. The room, with its scattered boxes and tapes, reflects his disorganized mind and the fragmentation of his memories. The den serves as both a physical and metaphorical prison, trapping Krapp in his past and emphasizing his detachment from the outside world. Its claustrophobic atmosphere underscores the themes of loneliness and existential despair, mirroring Krapp’s inner turmoil.

Reception and Impact

Critically acclaimed for its exploration of memory and existential themes, Krapp’s Last Tape has become a landmark in modern theater, influencing many playwrights and productions.

7.1 Critical Responses to the Play

Krapp’s Last Tape has received widespread critical acclaim for its exploration of memory, regret, and existential themes. Critics praise its minimalist structure and profound emotional depth, with many hailing it as a masterpiece of modern theater. The play’s ability to evoke introspection and discomfort has resonated with audiences, while its innovative use of the tape recorder as a narrative device has been particularly celebrated. Performances by Stephen Rea and Gary Oldman have further elevated its reputation, showcasing the versatility of Beckett’s work.

7.2 Influence on Modern Theater

Krapp’s Last Tape has significantly influenced modern theater through its innovative storytelling and minimalist approach. The play’s use of a single character and tape recordings has inspired many playwrights and directors to experiment with non-traditional narrative structures. Its exploration of memory and isolation continues to resonate, making it a benchmark for contemporary performances. The play’s impact is evident in its enduring popularity and adaptations, solidifying its place in theatrical history.

Notable Productions and Adaptations

Stephen Rea and Gary Oldman have delivered memorable performances in landmark productions of Krapp’s Last Tape, each bringing unique depth to the character.

8.1 Landmark Productions Featuring Stephen Rea

Stephen Rea’s portrayal of Krapp in Vicky Featherstone’s production is widely acclaimed for its emotional depth and nuance. The play, first staged in Dublin, captures Krapp’s existential despair with austerity and precision. Rea’s performance, marked by subtle expressions and poignant delivery, brings Beckett’s tragicomic character to life. The production’s minimalist design and haunting lighting emphasize Krapp’s isolation, creating a powerful theatrical experience.

8.2 Gary Oldman’s Interpretation of Krapp

Gary Oldman’s rendition of Krapp is a masterful solo performance, capturing the character’s descent into despair. His portrayal conveys Krapp’s inner turmoil through subtle facial expressions and vocal inflections. The production, designed and directed by Oldman himself, features stark visuals that amplify Krapp’s isolation. As the play progresses, Oldman’s physical transformation mirrors Krapp’s emotional disintegration, culminating in a haunting conclusion that lingers with the audience long after the lights dim.

Educational Resources and Further Reading

Krapp’s Last Tape is widely available in PDF format on platforms like the Internet Archive, offering free access to the play and other dramatic pieces by Beckett.

9.1 Availability of “Krapp’s Last Tape” in PDF Format

Krapp’s Last Tape is readily available in PDF format on platforms like the Internet Archive, where it can be downloaded for free as part of Beckett’s dramatic pieces collection.

Published in 1958, the play is accessible in various digital formats, including PDF, EPUB, and Kindle, making it easy for readers to explore this existential masterpiece and its themes of memory and isolation;

9.2 Recommended Secondary Sources and Analyses

Daniel Sack offers a comprehensive survey of Krapp’s Last Tape in his work, providing insights into its existential themes for a general audience.

Vivian Mercier’s critique of Beckett’s plays, including Krapp’s Last Tape, offers a deeper understanding of its cultural and philosophical significance.

ResearchGate and academic journals host numerous analyses, with over 25 million publications available for further exploration of the play’s themes and impact.

Krapp’s Last Tape is a haunting exploration of memory, regret, and the passage of time, capturing the essence of Beckett’s existential themes through Krapp’s solitary struggle.

10.1 Summary of Key Themes and Ideas

At its core, Krapp’s Last Tape examines memory, regret, and the inexorable passage of time. Krapp’s tapes symbolize his fragmented self, revealing a life of missed opportunities and existential despair. The play highlights loneliness, the futility of human endeavor, and the search for meaning in a seemingly meaningless world. Beckett’s work profoundly explores the human condition through Krapp’s poignant struggle with his past and mortality.

Bybeatrice

geopolitics: making sense of a changing world pdf

Understanding Geopolitics: An Overview

Geopolitics is the study of how geography‚ power‚ and politics shape international relations and global dynamics. It examines how nations interact‚ compete‚ and cooperate‚ influencing stability and conflict. By analyzing territorial disputes‚ resource distribution‚ and strategic alliances‚ geopolitics provides insights into the complexities of a rapidly changing world. It helps policymakers and scholars understand the interconnectedness of global challenges‚ offering frameworks to navigate power shifts and environmental pressures. This field is essential for grasping the intricacies of modern statecraft and its impact on global governance.

Defining Geopolitics

Geopolitics is the study of how geography‚ political power‚ and economic interests shape international relations and global dynamics. It examines how nations interact‚ compete‚ and cooperate‚ focusing on territorial disputes‚ resource distribution‚ and strategic alliances. Geopolitics explores how physical landscapes‚ cultural identities‚ and political ideologies influence state behavior and global stability. By analyzing these factors‚ it provides insights into power struggles‚ conflict resolution‚ and the pursuit of national interests. This discipline is crucial for understanding the complexities of a changing world‚ where geography and politics are deeply intertwined‚ shaping the trajectory of global governance and international affairs.

Historical Context and Evolution

Geopolitics emerged as a distinct field of study in the late 19th century‚ influenced by thinkers like Alfred Thayer Mahan and Halford Mackinder. It initially focused on territorial control and resource competition‚ shaping early 20th-century power struggles. The concept of “geopolitical determinism” gained prominence‚ suggesting that geography dictates national destiny. Over time‚ geopolitics evolved to incorporate economic‚ cultural‚ and ideological dimensions‚ particularly during the Cold War. Today‚ it addresses globalization‚ climate change‚ and technological advancements‚ reflecting a broader understanding of power dynamics. This evolution underscores how geopolitics adapts to changing global realities‚ remaining a critical lens for analyzing international relations.

Key Concepts in Geopolitical Analysis

Geopolitical analysis focuses on understanding power dynamics‚ territorial disputes‚ and resource competition. It examines how geography shapes national interests‚ alliances‚ and conflicts‚ while addressing economic and military strategies.

Geographical Determinism and Its Critics

Geographical determinism posits that physical geography shapes human behavior‚ culture‚ and political outcomes. Critics argue this oversimplifies complex interactions between environment and society‚ neglecting human agency and technological advancements. While geography influences resource distribution and strategic positions‚ it is not the sole determinant of national fate. Critics like Carl Sauer and Richard Hartshorne challenged determinism‚ emphasizing the role of culture and politics. Modern debates recognize geography’s role but stress the interplay of multiple factors. This critique highlights the need for a nuanced approach to understanding geopolitical dynamics‚ avoiding reductionist views that ignore historical and social contexts.

The Role of Power and Influence in International Relations

Power and influence are central to geopolitical dynamics‚ shaping how nations interact and compete. Hard power‚ such as military and economic strength‚ enables states to project influence globally. Soft power‚ including cultural and ideological appeal‚ fosters cooperation and allegiance. Emerging powers like China and India are reshaping global hierarchies‚ challenging traditional dominance. Influence is also exerted through international institutions and alliances‚ reflecting shifting balances of power. Understanding these mechanisms is crucial for analyzing contemporary geopolitics‚ as nations navigate a multipolar world where influence is contested and renegotiated continuously.

Modern Geopolitical Challenges

Today’s geopolitical landscape faces rapid shifts in global power‚ technological advancements‚ and environmental pressures‚ creating complex challenges for international stability and cooperation.

Climate Change and Resource Competition

Climate change has emerged as a critical geopolitical challenge‚ intensifying competition for scarce resources like water‚ energy‚ and arable land. Rising temperatures and extreme weather events disrupt economies and trigger migration‚ fueling tensions between nations. Resource-rich regions‚ such as the Arctic‚ are becoming contested zones due to melting ice and access to new trade routes; Meanwhile‚ countries are increasingly prioritizing energy security‚ shifting toward renewable sources but also vying for control of traditional fossil fuel reserves. These dynamics threaten global stability‚ as resource scarcity and environmental degradation exacerbate existing conflicts and reshape international alliances.

The Rise of Emerging Powers and Shifts in Global Influence

The rise of emerging powers‚ particularly in Asia and Africa‚ is reshaping global influence and challenging the existing world order. Countries like China‚ India‚ and Brazil are asserting their economic and political might‚ shifting the balance of power away from traditional Western dominance. This shift is evident in trade‚ technology‚ and military capabilities‚ as these nations increasingly influence global governance and multilateral institutions. The transition is not without tensions‚ as established powers resist ceding their dominance‚ leading to strategic rivalries and competition for resources. This dynamic is reshaping alliances and creating new opportunities and challenges for international cooperation and conflict.

Tools for Analyzing Geopolitical Dynamics

Mapping‚ spatial analysis‚ and economic indicators are essential tools for understanding geopolitical shifts‚ enabling the assessment of power dynamics‚ resource competition‚ and territorial influences in global affairs.

Mapping and Spatial Analysis

Mapping and spatial analysis are crucial tools in geopolitical studies‚ enabling the visualization of territorial boundaries‚ resource distribution‚ and strategic locations. These methods help identify patterns in global power dynamics‚ such as military bases‚ trade routes‚ and areas of conflict. By analyzing geographic data‚ policymakers can better understand how physical landscapes influence political decisions and international relations. Spatial analysis also aids in predicting potential flashpoints and assessing the impact of environmental changes on geopolitical stability. This approach provides a visual and data-driven framework for comprehending complex interactions between geography‚ power‚ and diplomacy in an increasingly interconnected world.

Economic and Military Indicators

Economic and military indicators are pivotal in assessing a nation’s geopolitical influence. GDP‚ trade balances‚ and resource control reflect economic strength‚ shaping global power dynamics. Military capabilities‚ including defense spending and technological advancements‚ signal a nation’s ability to project power. These indicators help analysts predict potential conflicts and alliances. For instance‚ rising military expenditures in emerging powers indicate shifting global influence. Economic sanctions and trade agreements also reveal geopolitical strategies. By monitoring these indicators‚ policymakers can anticipate threats and opportunities‚ ensuring informed decision-making in an increasingly competitive international landscape. These metrics are essential for understanding the interplay of power and economics in geopolitics.

Case Studies in Contemporary Geopolitics

Examining the Indo-Pacific region and the Ukraine-Russia conflict reveals how geopolitical tensions shape global stability‚ highlighting the intersection of power‚ territory‚ and international alliances in modern conflicts.

Eastern Europe and the Ukraine-Russia Conflict

The Ukraine-Russia conflict is a focal point of geopolitical tension‚ driven by historical ties‚ territorial disputes‚ and competing alliances. Russia’s annexation of Crimea in 2014 and ongoing support for separatist groups in eastern Ukraine have destabilized the region. NATO’s expansion into Eastern Europe has exacerbated tensions‚ with Russia perceiving it as a threat to its sphere of influence. The conflict highlights the complexities of post-Cold War geopolitics‚ where ethnic‚ political‚ and economic factors intertwine‚ shaping the balance of power in Europe and beyond. It underscores the challenges of maintaining regional stability amidst great power rivalry.

The Indo-Pacific Region and Strategic Rivalries

The Indo-Pacific region has emerged as a critical geopolitical hotspot‚ marked by intensifying strategic rivalries. The U.S.-China competition dominates the landscape‚ with both powers vying for influence over trade routes‚ military alliances‚ and economic partnerships. India’s rise as a regional power further complicates dynamics‚ as it seeks to counterbalance China’s expanding presence. The Quad grouping and regional security pacts highlight the growing importance of multilateral cooperation. Territorial disputes in the South China Sea and economic competition add layers of tension. This region is pivotal in shaping the future of global power dynamics and international relations.

The Future of Geopolitics

Technological advancements and shifting power dynamics will reshape global relations‚ emphasizing sustainability and multilateral cooperation to address emerging challenges and ensure a stable international order.

Technological Advancements and Their Impact

Technological advancements are reshaping geopolitics‚ with innovations like artificial intelligence‚ cyber warfare‚ and space exploration altering global power dynamics. These technologies enable nations to project influence beyond traditional territorial boundaries‚ creating new arenas for competition and cooperation. The rise of digital surveillance and data-driven decision-making further complicates international relations‚ as countries strive to maintain sovereignty and security in an increasingly interconnected world. Meanwhile‚ emerging technologies like renewable energy systems and autonomous weapons challenge existing geopolitical strategies‚ forcing nations to adapt and redefine their roles in a rapidly evolving global landscape.

The Role of Non-State Actors and Global Governance

Non-state actors‚ such as multinational corporations‚ NGOs‚ and cyber groups‚ play a significant role in shaping modern geopolitics. These entities often wield considerable influence‚ bypassing traditional state-centric systems. They can impact global governance by lobbying for policy changes‚ controlling resources‚ or disseminating information. The rise of non-state actors challenges the dominance of nation-states‚ creating new power dynamics. This shift compels governments to adapt and collaborate more effectively with these entities to address global challenges. As a result‚ the interplay between state and non-state actors becomes increasingly critical in shaping international relations and the future of global governance.

Geopolitics remains a dynamic field‚ shaping global interactions and power dynamics. Understanding its complexities is crucial for navigating an increasingly interconnected world‚ ensuring informed decision-making and sustainable strategies.

Summarizing Key Insights

Geopolitics is a dynamic field that examines the interplay of geography‚ power‚ and politics in shaping global interactions. Key insights include the role of resource competition‚ territorial disputes‚ and emerging powers in reshaping international relations. Climate change and technological advancements further complicate these dynamics‚ demanding adaptive strategies. Understanding these elements is crucial for addressing contemporary challenges‚ from regional conflicts to economic shifts. By analyzing these factors‚ policymakers and scholars can better navigate the complexities of a changing world‚ fostering cooperation and stability in an increasingly interconnected global landscape.

Implications for Policymakers and Scholars

Geopolitical analysis provides critical insights for policymakers and scholars‚ enabling informed decision-making in a rapidly evolving global landscape. Understanding power dynamics‚ resource competition‚ and territorial disputes allows policymakers to craft adaptive strategies that mitigate conflicts and foster cooperation. Scholars benefit from geopolitical frameworks to identify patterns and predict future challenges‚ offering academic rigor to real-world issues. Together‚ these insights promote a deeper understanding of global stability and instability‚ aiding in the development of policies that address environmental‚ economic‚ and security challenges. This collaborative approach ensures that geopolitical knowledge remains a cornerstone of effective governance and academic research.

Bybeatrice

asme b31.3 pdf

ASME B31.3 is a critical standard for pressure piping systems, ensuring safety and reliability in design, materials, and fabrication. It guides the construction of piping systems across industries.

Overview of the Standard

ASME B31.3 provides comprehensive guidelines for designing, fabricating, and testing metallic pressure piping systems. It ensures safety, reliability, and compliance across industries like chemical, oil, and gas. The standard covers pipe wall thickness calculations, material selection, welding practices, and stress analysis. It also addresses flexibility and support systems to prevent failure under operational stresses. Adherence to B31.3 is crucial for engineers to design and maintain piping systems efficiently and safely.

Importance of ASME B31.3 in Pressure Piping

Importance of ASME B31;3 in Pressure Piping

ASME B31.3 ensures pressure piping systems are safe, efficient, and compliant with industry standards. It minimizes risks of failure, protecting people and the environment. By standardizing design, materials, and practices, it fosters consistency and reliability. Compliance with B31.3 enhances system performance and longevity, making it indispensable for engineers and organizations in industries like oil, gas, and chemical processing.

Key Components of ASME B31.3

ASME B31.3 outlines design requirements, material specifications, fabrication practices, and testing procedures for pressure piping systems. It ensures compliance with safety standards and industry regulations.

Design Requirements and Calculations

ASME B31.3 provides detailed design requirements and calculation methods for pressure piping systems. It covers pipe wall thickness determination, stress analysis, and flexibility considerations. The standard ensures piping systems can withstand operational stresses, including pressure, temperature, and mechanical loads. Calculations must adhere to specified formulas and guidelines to guarantee system integrity and safety. Compliance with these requirements is essential for reliable operation.

Material Specifications and Selection

ASME B31.3 outlines strict material specifications and selection criteria for pressure piping. It classifies materials based on their mechanical properties, temperature limits, and corrosion resistance. The standard ensures materials are suitable for specific service conditions, enhancing system durability and safety. Proper material selection is critical to prevent failures and ensure compliance with design and operational requirements.

Fabrication and Testing Practices

ASME B31.3 provides detailed fabrication and testing practices to ensure piping system integrity. It outlines welding procedures, non-destructive testing methods, and allowable defect tolerances. The standard also covers cutting practices and post-weld heat treatment. Compliance with these guidelines ensures the safety and reliability of pressure piping systems by maintaining material properties and structural soundness throughout the fabrication process.

Historical Background and Development

ASME B31.3 originated from earlier piping standards, evolving to address advancing technologies and safety needs. Its development began with the 1942 ASA B31.1 code, later refined into B31.3.

Evolution of the B31.3 Code

The ASME B31.3 code evolved from earlier standards, with its roots in the 1942 ASA B31.1 code. Initially published as B31.3 in 1955, it has undergone numerous revisions to address technological advancements and industry needs; Updates have focused on enhancing safety, design accuracy, and material specifications, ensuring the code remains a cornerstone for pressure piping systems globally.

Significant Revisions and Updates

ASME B31.3 has undergone significant updates to reflect industry advancements and safety requirements. Recent revisions include enhanced material verification processes and alignment with global standards like PED 2014/68/EU. Updates in 2024 introduced stricter guidelines for design calculations and fabrication practices, ensuring compliance with international regulations. These changes highlight the code’s continuous evolution to address emerging challenges in pressure piping systems;

Flexibility and Support of Piping Systems

ASME B31.3 emphasizes the importance of piping flexibility to prevent stress-related damage. Proper support systems, including spring supports, ensure structural integrity and safety under operating conditions.

Understanding Flexibility in Piping Design

Flexibility in piping design ensures systems can absorb thermal expansion and mechanical loads without failure. ASME B31.3 provides guidelines for calculating flexibility to prevent stress-related damage, ensuring safe operation.

Types of Pipe Supports and Their Applications

ASME B31.3 outlines various pipe supports, including rigid, spring, and variable supports. Rigid supports prevent movement, while spring supports allow for thermal expansion. Variable supports adjust to system needs. Proper selection ensures weight distribution, reduces stress, and prevents damage. The code provides sizing procedures and application guidelines for these supports, ensuring system integrity and safety in diverse piping environments.

Compliance with International Standards

ASME B31.3 aligns with international standards like EN 13480 and PED 2014/68/EU, promoting harmonization and ensuring compliance with global piping regulations for safety and reliability.

Comparison with EN 13480 and PED 2014/68/EU

ASME B31.3 differs from EN 13480 and PED 2014/68/EU in specific requirements. EN 13480-7 exceeds B31.3 by mandating EU Member State-designated organizations for verification. PED 2014/68/EU focuses on essential safety requirements, while B31.3 provides detailed design and fabrication guidelines. These differences highlight the need for careful compliance when aligning ASME standards with European regulations for global piping projects.

Harmonization of ASME B31.3 with Global Regulations

ASME B31.3 is increasingly aligned with global standards to facilitate international projects. While primarily a U.S. code, it is recognized worldwide for its comprehensive guidelines. Efforts to harmonize its requirements with international standards like ISO and EAC ensure consistency. This collaboration enables engineers to apply ASME B31.3 in global contexts, streamlining compliance and reducing design complexities across borders while maintaining safety and reliability.

Role of the Design Authority

The Design Authority is responsible for specifying design parameters, ensuring compliance with ASME B31.3, and maintaining safety in piping systems throughout the project lifecycle.

Responsibilities in Determining Design Parameters

The Design Authority is tasked with defining design criteria, selecting materials, and ensuring compliance with ASME B31.3. This includes specifying pressure-temperature limits, calculating pipe wall thickness, and conducting stress analysis to ensure piping integrity and safety. They must also verify that all design parameters align with the standard’s requirements and industry best practices, ensuring the system’s reliability and performance under operational conditions.

Ensuring Compliance and Safety in Piping Systems

Compliance with ASME B31.3 is critical for ensuring the safety and reliability of piping systems. The Design Authority must verify that all design parameters, materials, and fabrication practices meet the standard’s requirements. This includes conducting thorough stress analysis, testing, and inspections to prevent failures. Adherence to the code ensures that piping systems operate safely under various conditions, aligning with international standards like EN 13480 and PED 2014/68/EU for enhanced safety and regulatory compliance.

Calculations and Stress Analysis

ASME B31.3 provides detailed methods for pipe wall thickness determination and stress analysis to ensure piping systems withstand operational pressures and stresses safely and reliably.

Methods for Pipe Wall Thickness Determination

ASME B31.3 provides formulas to calculate pipe wall thickness, considering factors like pressure, temperature, and corrosion allowance. These calculations ensure piping systems can safely withstand operational stresses while maintaining efficiency and durability.

Stress Analysis Procedures for Safe Design

ASME B31.3 outlines detailed stress analysis procedures to ensure piping systems can withstand operational stresses. These include evaluating bending, torsional, and axial stresses. The code provides guidelines for calculating stress intensities and allowable limits, ensuring compliance with safety standards. By following these procedures, designers can identify potential failure points and optimize piping layouts for safe and reliable performance under various operating conditions.

Fabrication and Installation Guidelines

ASME B31.3 establishes rules for welding, cutting, and installation of piping systems. It ensures proper techniques, inspection, and compliance with safety standards, minimizing risks during operation.

Welding and Cutting Practices

ASME B31.3 specifies detailed requirements for welding and cutting in pressure piping systems. Techniques like SMAW, GTAW, and FCAW are standardized to ensure joints meet strength and integrity criteria. The code emphasizes proper preheating, post-weld heat treatment, and non-destructive examination (NDE) to verify weld quality. These practices minimize defects, ensuring safe and reliable piping installations across various industrial applications.

Installation Considerations for Piping Systems

ASME B31.3 provides comprehensive guidelines for installing piping systems, emphasizing alignment, support, and stress management. Proper handling of thermal expansion and contraction is crucial to prevent damage. The code also addresses environmental factors, such as corrosion protection and insulation, ensuring long-term system integrity and operational safety across diverse industrial environments.

Documentation and Record-Keeping

Proper documentation ensures compliance, traceability, and maintenance of piping systems. ASME B31.3 requires detailed records of design, fabrication, testing, and inspection for future reference and audits.

Importance of Proper Documentation

Proper documentation ensures compliance with ASME B31.3 standards, providing traceability and accountability. It facilitates audits, maintenance, and future modifications, ensuring safety and reliability in piping systems. Detailed records of design, fabrication, and testing are essential for compliance and operational integrity.

Record-Keeping Requirements for Compliance

ASME B31.3 mandates detailed record-keeping to ensure compliance with design, fabrication, and testing standards. Records must include material specifications, welding procedures, and test results. Proper documentation ensures traceability and accountability, facilitating audits and compliance verification. Adherence to these requirements is critical for maintaining safety, operational integrity, and regulatory conformity in pressure piping systems. The Design Authority must verify and maintain these records for future reference and inspections.

ASME B31.3 remains a cornerstone for pressure piping safety and efficiency. Future updates will likely incorporate emerging technologies and innovative solutions to address evolving industry challenges and standards.

ASME B31.3 provides comprehensive guidelines for designing, fabricating, and testing pressure piping systems, ensuring safety and compliance. It covers material selection, stress analysis, and fabrication practices. The standard emphasizes the role of the Design Authority in determining parameters and ensuring compliance. Key takeaways include understanding flexibility, support systems, and the importance of proper documentation. Future updates will focus on harmonizing with global standards and incorporating new technologies to address evolving industry needs and challenges.

Future Trends in Pressure Piping Design

Emerging technologies like AI and additive manufacturing are reshaping pressure piping design. ASME B31.3 is expected to integrate advanced materials and digital tools for enhanced safety and efficiency. There will be a greater emphasis on sustainability and energy efficiency in piping systems. Additionally, the standard will likely adopt more stringent requirements to align with global regulations, ensuring harmonized practices across industries. These trends aim to meet future challenges effectively.

Additional Resources

Access the ASME B31.3 PDF through official ASME platforms or authorized distributors. Explore supplementary guides and webinars for comprehensive understanding and practical applications of the standard.

Where to Find ASME B31.3 PDF

The ASME B31.3 PDF can be accessed through the official ASME website or authorized distributors. It is also available on select online marketplaces and engineering resource platforms. Ensure purchases are made from reputable sources to guarantee authenticity and compliance with copyright laws. Additionally, many engineering libraries and institutions provide access to the standard for reference purposes.

fire safety test questions and answers pdf

Fire safety is a critical life skill, and understanding its principles can mean the difference between life and death. This quiz provides essential knowledge on fire prevention, evacuation procedures, and emergency techniques. It covers key topics like fire causes, extinguisher types, and safety drills, helping individuals and organizations stay prepared. The questions are designed to test awareness and promote practical application, ensuring everyone can act confidently in fire-related situations.

By engaging with these questions, participants can identify gaps in their knowledge and improve their ability to respond effectively during emergencies. Whether at home, school, or work, this quiz serves as a valuable tool for fostering a culture of fire safety and readiness.

1.1 Importance of Fire Safety Education

Fire safety education empowers individuals with knowledge to prevent fires, respond effectively, and protect lives. It fosters awareness of potential hazards, proper use of equipment, and emergency procedures. Regular training and quizzes ensure preparedness, reducing panic during incidents. Educating communities, especially children and employees, builds a culture of safety, minimizing risks and saving lives. Knowledgeable individuals are better equipped to act calmly and responsibly in fire emergencies.

1.2 Benefits of Using Quizzes for Fire Safety Training

Quizzes enhance fire safety training by engaging participants and reinforcing knowledge. They help identify gaps in understanding, ensuring better retention of critical safety practices. Interactive and accessible, quizzes make learning enjoyable while preparing individuals for real-life emergencies. Regular use of fire safety quizzes fosters confidence and readiness, benefiting both home and workplace environments.

Common Causes of Fires

Fires often result from electrical issues, unattended flames, and human error. Key causes include faulty wiring, kitchen mishaps, and improper use of appliances or smoking materials nearby.

2.1 Identifying Potential Fire Hazards

Identifying fire hazards is crucial for preventing accidents. Common risks include unattended candles, overloaded electrical outlets, and improperly stored flammable materials. Regular inspections can help spot these dangers early, allowing for corrective actions like proper storage of chemicals and ensuring all electrical systems are up to code. Awareness and vigilance are key to maintaining a safe environment and reducing fire risks effectively.

2.2 Preventing Fires in Home and Workplace

Preventing fires involves proactive measures like installing smoke detectors, avoiding electrical overload, and storing flammable materials safely. Regular inspections of appliances and wiring are essential to spot potential risks. Ensuring proper ventilation, avoiding clutter, and maintaining fire extinguishers can also mitigate hazards. Educating everyone on fire risks and promoting safe practices fosters a culture of prevention, reducing the likelihood of fires in both home and workplace settings.

Fire Extinguisher Operation and Types

Understanding fire extinguisher types and their operation is crucial for effective fire control. Classes A, B, C, D, and K extinguishers target specific fire sources, from ordinary combustibles to electrical and chemical fires. Proper techniques ensure safe and efficient use, preventing fires from escalating. Regular training and accessibility of extinguishers are key to maintaining fire safety in any setting.

Using the wrong extinguisher can worsen a fire, so identifying the fire class is essential. Always follow the PASS method: Pull the pin, Aim the nozzle, Squeeze the handle, and Sweep the extinguishing agent. Proper maintenance and inspections ensure extinguishers are ready for emergencies.

3.1 Understanding Fire Extinguisher Classes (A, B, C, D, K)

Fire extinguishers are classified based on the types of fires they combat. Class A extinguishers handle ordinary combustibles like paper and wood. Class B is for flammable liquids such as gasoline or oil. Class C is designed for electrical fires, while Class D tackles metal fires. Class K extinguishers are specifically for cooking oils and greases. Each class requires a unique approach to safely and effectively extinguish the fire.

Understanding these classifications ensures the correct extinguisher is used, preventing fire escalation. Using the wrong type can worsen the situation, making it crucial to identify the fire class before acting. Proper training and knowledge of these classes are essential for effective fire management.

3.2 Proper Techniques for Using Fire Extinguishers

Proper techniques for using fire extinguishers are crucial for effective fire management. The PASS method—Pull, Aim, Squeeze, Sweep—provides a systematic approach to extinguishing fires safely.

Pull the safety pin, aim at the base, squeeze to release the agent, and sweep from side to side. Ensure the extinguisher is accessible and know its limitations to prevent fire escalation.

Emergency Procedures During a Fire

Emergency procedures during a fire involve quick action and clear thinking. Establishing an evacuation plan, identifying exits, and staying low to avoid smoke are critical steps. Always prioritize safety and follow designated escape routes to ensure a swift and secure exit during a fire emergency.

4.1 Creating an Evacuation Plan

Creating a fire evacuation plan is crucial for ensuring safety during emergencies. Identify escape routes, designate a meeting point outside, and practice drills regularly. Clearly mark exits and ensure all occupants understand the plan. Tailor it to specific needs, such as mobility challenges, and update it as conditions change. A well-prepared plan reduces confusion and saves lives during a fire.

4.2 Stop, Drop, and Roll Technique

The Stop, Drop, and Roll technique is essential for extinguishing flames on the body. If your clothing catches fire, stop moving, drop to the ground, and roll to smother the flames. This method prevents oxygen from fueling the fire and minimizes burns. Never run, as it spreads the fire. Always cover your face to protect from heat and smoke. Practice this lifesaving technique regularly.

Fire Safety Equipment and Maintenance

Smoke detectors, fire extinguishers, and alarms are vital equipment for early fire detection and suppression. Regular inspections and maintenance ensure they function properly during emergencies, saving lives.

5.1 Smoke Detectors and Alarms

Smoke detectors are crucial for early fire detection, significantly reducing risks in emergencies. Install them on every level of your home and inside sleeping areas. Test them monthly and replace batteries twice a year. Avoid installing in kitchens to prevent false alarms. A functioning smoke detector can save lives by providing critical early warnings. Regular maintenance ensures reliability and effectiveness in case of fire.

5.2 Importance of Regular Fire Safety Inspections

Regular fire safety inspections are vital for identifying and addressing potential hazards. They ensure compliance with safety standards, prevent fire risks, and protect lives and property. Inspections include checking fire extinguishers, smoke detectors, and escape routes. By conducting these checks, organizations and homeowners can maintain a safe environment and respond effectively in emergencies. Consistent inspections foster preparedness and accountability, minimizing fire-related incidents and their consequences.

Fire Prevention Tips and Best Practices

Prevent fires by installing smoke detectors, avoiding electrical overloads, storing flammable materials safely, and conducting regular inspections. These practices minimize risks and ensure a safer environment.

6.1 Safe Use of Electrical Appliances

To prevent fires, avoid overloading outlets with too many devices, as this can cause overheating. Use extension cords wisely and never run them under rugs or near water. Keep electrical appliances away from flammable materials like curtains or paper. Regularly inspect cords and plugs for damage, and replace worn-out items promptly. Always follow manufacturer guidelines for proper usage.

Avoid using damaged or frayed cords.
Keep appliances away from water and heat sources.
Unplug devices when not in use to reduce standby power consumption.

By adhering to these practices, you can significantly reduce the risk of electrical fires and ensure a safer living or working environment.

6.2 Proper Storage of Flammable Materials

Store flammable liquids and materials in well-ventilated, designated areas away from heat sources and open flames. Use approved containers with tight-fitting lids to prevent vapors from escaping. Label containers clearly and keep them away from incompatible substances. Ensure storage areas are cool, dry, and protected from sparks or ignition sources. Always follow safety guidelines to minimize fire risks.

Keep flammable materials away from direct sunlight.
Use fire-resistant storage cabinets when possible.
Adhere to local fire codes and regulations.

Fire Safety Drills and Preparedness

Fire safety drills ensure preparedness by simulating real-life scenarios, teaching evacuation routes, and testing emergency procedures. Regular practice helps individuals respond calmly and efficiently during fires.

7.1 Conducting Fire Safety Drills at Home

Fire safety drills at home are essential for preparing family members to respond quickly and calmly during emergencies. Identify at least two escape routes from each room and designate a safe meeting spot outside the home. Practice the drills every 6 months, involving children and teaching them the Stop, Drop, and Roll technique. Ensure everyone understands the plan and simulates real-life conditions, such as darkness or smoke, to enhance preparedness.

7;2 Training Employees on Fire Emergency Response

Effective fire emergency response training for employees ensures a safe and organized reaction during incidents. Employers should conduct regular drills, educate staff on fire extinguisher use, and establish clear evacuation routes. Training should include identifying fire hazards, understanding alarm systems, and knowing emergency contact procedures. Regular updates on safety protocols and encouraging employee participation in mock drills enhance preparedness and minimize risks in the workplace.

Fire Safety in Specific Settings

Fire safety practices differ across homes, workplaces, and schools based on unique hazards. Tailored strategies ensure preparedness. Regular drills and education are crucial for safety.

8.1 Fire Safety at Home

Home fire safety requires proactive measures to protect families. Installing smoke detectors, securing electrical systems, and storing flammable materials safely are essential. Regular fire drills ensure everyone knows escape routes. Teaching children fire hazards and the Stop, Drop, and Roll technique is vital. Maintaining fire extinguishers and avoiding overloading outlets further reduce risks. Preparedness at home can prevent tragedies.

8.2 Fire Safety in the Workplace

Workplace fire safety involves creating a secure environment through prevention and preparedness. Employers must implement fire prevention programs and inform employees of hazards. Regular fire drills, emergency exit plans, and proper storage of flammable materials are essential. Understanding fire extinguisher types ensures effective response. Training employees on emergency procedures and conducting regular inspections further enhance workplace safety, reducing risks and ensuring compliance with safety standards.

8.3 Fire Safety in Schools

Fire safety in schools is crucial to protect students, staff, and facilities; Schools must conduct regular fire drills, ensuring everyone knows escape routes and assembly points. Educating students on fire hazards and proper evacuation procedures is essential. Schools should maintain functional fire alarms, clear emergency exits, and conduct regular inspections to prevent fire hazards. Training staff and students ensures preparedness and quick response during emergencies, safeguarding the school community.

Advanced Fire Safety Topics

Advanced fire safety topics include understanding fire behavior, managing complex emergencies, and handling specialized fires like electrical or chemical fires. These topics require in-depth knowledge and training to ensure effective response and mitigation, critical for safeguarding lives and property in high-risk environments;

9.1 Understanding Fire Classes and Their Hazards

Fire classes (A, B, C, D, K) are categorized based on fuel sources and hazards. Class A involves ordinary combustibles like wood or paper, while Class B includes flammable liquids. Class C pertains to electrical fires, and Class D involves combustible metals. Class K is for kitchen fires involving cooking oils. Understanding these classes is crucial for selecting the right extinguishing agents and safely managing fire incidents.

9.2 Handling Electrical and Chemical Fires

Electrical fires require caution, as water can conduct electricity, worsening the situation. Use Class C extinguishers for electrical fires. Chemical fires demand specialized agents based on the substance involved. Always evacuate the area, wear protective gear, and avoid using incompatible extinguishing methods. Proper training is essential to handle such hazardous situations safely and effectively, minimizing risks and preventing further damage or injury.

Resources for Fire Safety Quiz Questions and Answers

Reliable PDF materials and online platforms provide comprehensive guides, practice tests, and detailed solutions for fire safety quizzes. These resources are essential for effective study and training preparation.

10.1 Where to Find Reliable Fire Safety PDF Materials

Reliable fire safety PDF materials can be found on websites like hsestudyguide.com, which offers comprehensive guides and practice tests. Educational institutions and fire safety organizations also provide free downloadable resources. Additionally, platforms like Google Drive and Scribd host shared PDFs, while official fire safety organizations like NFPA publish detailed guides. Always verify the credibility of the source to ensure accuracy and relevance.

10.2 Online Platforms for Fire Safety Quizzes

Popular online platforms like Quizlet, SafetyCulture, and hsestudyguide.com offer free fire safety quizzes. These platforms provide interactive tests, multiple-choice questions, and downloadable PDF materials. They cover topics like fire prevention, evacuation procedures, and extinguisher usage. Many also offer customizable tests, making them ideal for both individual learning and workplace training. These resources are accessible and user-friendly, ensuring comprehensive fire safety knowledge.

Bybeatrice

consecration to st joseph fr calloway pdf

Consecration to St․ Joseph, popularized by Fr․ Donald Calloway, is a spiritual act of entrusting oneself to his paternal care, following a structured program of prayer and reflection․

Overview of Consecration to St․ Joseph

Consecration to St․ Joseph is a spiritual act of entrustment, where individuals dedicate themselves to his paternal care, seeking his guidance and protection․ Popularized by Fr․ Donald Calloway, this practice involves a structured program of prayer and reflection, often spanning 30 or 33 days, to prepare the heart for the formal act of consecration․ The process emphasizes the importance of St; Joseph’s virtues, such as humility, obedience, and fatherly love, and encourages believers to imitate these qualities in their daily lives․ Through this consecration, individuals entrust their spiritual well-being, families, and life decisions to St․ Joseph’s intercession, fostering a deeper relationship with him as their spiritual father․ The ultimate goal is to live a life more closely aligned with Christ, under the loving patronage of St․ Joseph․

Significance of St․ Joseph in Catholic Spirituality

St․ Joseph holds a profound place in Catholic spirituality as the earthly father of Jesus and the spouse of the Blessed Virgin Mary․ His virtues of humility, trust in God, and selfless love make him a powerful model for Christian living․ As the patron of the universal Church, St․ Joseph is often invoked for protection, guidance, and intercession in family life and vocational discernment․ His role as a father and caregiver exemplifies divine fatherhood, offering believers a tangible example of God’s providential love․ In consecration, St․ Joseph’s significance deepens as he is seen as a spiritual father, guiding individuals toward holiness and fostering a closer relationship with Christ․ His silent yet faith-filled life inspires believers to embrace humility, obedience, and surrender to God’s will, making him a cornerstone in Catholic devotion and spirituality․

Fr․ Donald Calloway’s Role in Promoting Consecration

Fr․ Donald Calloway has played a pivotal role in popularizing consecration to St․ Joseph through his book, Consecration to St․ Joseph: The Wonders of Our Spiritual Father․ His work provides a structured program for individuals to deepen their devotion, emphasizing prayer, reflection, and filial entrustment․ By highlighting St․ Joseph’s paternal care and spiritual fatherhood, Fr․ Calloway has made this devotion accessible to many, fostering a renewed appreciation for the saint’s role in Catholic spirituality․ His advocacy has inspired countless believers to seek St․ Joseph’s guidance, transforming lives and strengthening faith․ Fr․ Calloway’s efforts have been instrumental in spreading the devotion, making it a meaningful practice for modern Catholics seeking spiritual growth and protection under St․ Joseph’s patronage․

The Meaning and Purpose of Consecration

Consecration to St․ Joseph is a spiritual act of entrusting oneself to his paternal care, seeking his guidance, protection, and intercession for a deeper, holier life․

What is Consecration to St․ Joseph?

Consecration to St․ Joseph is a spiritual act of entrusting oneself to his paternal care, seeking his guidance, protection, and intercession․ It involves a formal prayer or commitment, where one dedicates their life, decisions, and spiritual growth to St․ Joseph’s guardianship․ This consecration is rooted in the belief that St․ Joseph, as the earthly father of Jesus and the Virgin Mary, offers a powerful model of faith, humility, and devotion․ By consecrating oneself to St․ Joseph, individuals aim to live a life more deeply rooted in faith, trusting in his intercession and paternal care․ This practice, popularized by Fr․ Donald Calloway, is often structured through specific prayers and reflections, emphasizing the desire to follow St․ Joseph’s virtues and seek his aid in spiritual and temporal matters․

The Spiritual Act of Filial Entrustment

The spiritual act of filial entrustment to St․ Joseph is a profound expression of devotion, where one entrusts their life, soul, and spiritual journey to his paternal care․ This act is rooted in the belief that St․ Joseph, as the earthly father of Jesus, possesses a unique role in guiding and protecting believers․ By surrendering oneself to his guardianship, individuals seek to imitate the trust and obedience that St․ Joseph demonstrated in his life․ This entrustment is not merely a symbolic gesture but a lived commitment, where one invites St․ Joseph to influence their decisions, strengthen their faith, and lead them closer to God․ Fr․ Donald Calloway emphasizes that this act deepens one’s relationship with St․ Joseph, fostering a spiritual fatherhood that enriches the Christian life and provides solace in times of need․

Benefits of Consecrating Oneself to St․ Joseph

Consecrating oneself to St․ Joseph offers numerous spiritual benefits, including a deeper connection to God and a strengthened faith life․ This act invites St․ Joseph’s paternal guidance, fostering a sense of protection and trust in his intercession․ Believers often experience spiritual clarity, courage, and strength in overcoming life’s challenges․ St․ Joseph’s role as a protector and provider extends to those who consecrate themselves, offering peace and confidence in daily life․ Additionally, this consecration can lead to a greater devotion to the Holy Family, inspiring virtues like humility, purity, and integrity․ Many also report experiencing miraculous graces, such as healing or provision, through St․ Joseph’s intercession․ Ultimately, consecration to St․ Joseph enriches one’s spiritual journey, offering a powerful means to grow in holiness and draw closer to Christ․

Preparing for Consecration

Preparing for consecration involves following a structured program of prayer and reflection, fostering a deep spiritual connection and trust in St․ Joseph’s guidance․

The Importance of Preparation

Preparation for consecration to St․ Joseph is essential to deepen one’s devotion and understanding of his role as a spiritual father․

It involves prayer, reflection, and entrustment, fostering a meaningful connection with St․ Joseph’s virtues and intercession․

Father Donald Calloway’s book provides a structured program, guiding individuals through this sacred process with intentionality and grace․

Through preparation, one readies their heart to fully embrace the spiritual act of entrustment, ensuring a lifelong commitment to living under St․ Joseph’s paternal care․

Following a Structured Program

Father Donald Calloway’s consecration to St․ Joseph is guided by a structured program, typically lasting 30 days, which includes daily prayers, reflections, and readings․

This program helps individuals prepare their hearts and minds for the act of consecration, fostering a deeper understanding of St․ Joseph’s role as a spiritual father․

By following the structured program, participants are able to gradually entrust themselves to St․ Joseph’s care, imitating his virtues and seeking his intercession in their lives․

The program emphasizes the importance of consistency and intentionality, ensuring that the consecration is not merely a one-time event but a lifelong commitment to living under St․ Joseph’s paternal guidance․

This structured approach provides a clear and meaningful path for those seeking to deepen their devotion and trust in St․ Joseph․

The Role of Prayer and Reflection

Prayer and reflection are central to the consecration process, serving as the foundation for deepening one’s relationship with St․ Joseph․ Through daily prayers and meditative reflection, individuals grow in understanding of his virtues and intercessory power․ The structured program often includes specific prayers and scriptural readings, guiding participants to seek St․ Joseph’s guidance․ Reflection helps internalize his paternal care, fostering trust and surrender․ This spiritual practice prepares the heart for the formal act of consecration, inviting St․ Joseph to influence every aspect of life․ By engaging in prayer and reflection, individuals experience a transformative journey, drawing closer to St․ Joseph and his divine mission․

The Act of Consecration

The act of consecration involves a formal prayer, typically on the final day of preparation, where one entrusts their life to St․ Joseph’s paternal care and guidance․

The Final Day of Preparation

The final day of preparation for consecration to St․ Joseph is a sacred moment of spiritual readiness․ It marks the culmination of a structured program, often lasting 30 or 33 days, during which one deeply reflects on St․ Joseph’s virtues and role in the Holy Family․ On this day, individuals typically attend Mass, participate in prayer, and engage in heartfelt reflection to prepare their souls for the act of consecration․ Fr․ Donald Calloway emphasizes the importance of a contrite heart and complete surrender to St․ Joseph’s paternal care․ This day is not just a ritual but a profound encounter with the Holy Spirit, inviting St․ Joseph to guide and protect one’s life․ It is a time to renew faith, trust, and devotion, ensuring readiness to formally entrust oneself to St․ Joseph’s loving fatherhood․

The Formal Prayer of Consecration

The formal prayer of consecration to St․ Joseph is the climactic moment of the spiritual journey, where one solemnly entrusts themselves to his paternal care․ This prayer, often recited on the final day of preparation, expresses a deep commitment to living under St․ Joseph’s guidance and protection․ It involves acknowledging his role as a spiritual father and seeking his intercession in all aspects of life․ Fr․ Donald Calloway emphasizes that this prayer is not merely a ritual but a heartfelt act of filial entrustment․ By reciting the prayer, individuals surrender their lives, families, and intentions to St․ Joseph, imploring him to “rule my soul and teach me the interior life․” This act is a profound expression of trust and devotion, inviting St․ Joseph to be a constant presence in one’s spiritual journey․

Living Out the Consecration

Living out the consecration to St․ Joseph is a lifelong commitment to embrace his spiritual fatherhood and guidance․ It involves integrating his virtues, such as humility, obedience, and fidelity, into daily life․ By fostering a deep devotion to St․ Joseph, individuals strive to imitate his faithfulness to God and his family․ This commitment is expressed through daily prayer, seeking his intercession, and trusting in his paternal care․ Fr․ Donald Calloway emphasizes that consecration is not a one-time act but a continuous journey of surrender and growth․ It requires ongoing reflection, prayer, and a willingness to follow St․ Joseph’s example in living a life of love, service, and holiness․ By living out the consecration, individuals draw closer to God and find strength in St․ Joseph’s protection and guidance․

Bybeatrice

printable nursing report sheet pdf

Printable nursing report sheets are essential tools for nurses to organize patient information‚ streamline shift reports‚ and enhance communication. These templates‚ available in formats like PDF‚ provide structured sections for documenting patient details‚ medications‚ and vital signs‚ ensuring clarity and efficiency in healthcare settings.

1.1 What is a Printable Nursing Report Sheet?

A printable nursing report sheet is a pre-designed template used by nurses to document patient information‚ vital signs‚ medications‚ and care plans. Available in formats like PDF‚ these sheets are filled out during shift changes‚ ensuring accurate handoffs and organized patient data. They are customizable‚ offering sections for demographics‚ assessments‚ and progress notes‚ making them indispensable for efficient and clear communication in healthcare settings.

1.2 Importance of Nursing Report Sheets in Healthcare

Nursing report sheets are vital for maintaining organization and consistency in patient care documentation. They improve communication during shift changes‚ ensuring continuity of care. By capturing essential patient data‚ these sheets enhance patient safety‚ reduce errors‚ and save time. They also provide a clear record of treatments and outcomes‚ supporting accurate documentation and better decision-making in healthcare settings.

1.3 How to Use a Nursing Report Sheet Effectively

Start by initiating the report sheet at the beginning of your shift during handoff. Document patient information‚ medications‚ vital signs‚ and assessments clearly. Ensure all details are accurate and up-to-date. Use the sheet to organize your thoughts and prioritize tasks. Review and update it throughout your shift‚ then communicate key points during handoff to the next nurse. This ensures continuity of care and improves patient outcomes.

Benefits of Using Printable Nursing Report Sheets

Printable nursing report sheets enhance efficiency‚ accuracy‚ and communication. They save time‚ reduce documentation errors‚ and provide a clear‚ organized format for patient information‚ improving overall care quality.

2.1 Enhanced Efficiency in Patient Care

Printable nursing report sheets streamline patient care by providing organized‚ quick-access documentation. Nurses can efficiently update and review patient details‚ reducing time spent on paperwork and allowing more focus on direct care. Pre-designed sections and checkboxes simplify data entry‚ ensuring critical information is captured swiftly. This structured approach minimizes delays and errors‚ enabling healthcare professionals to prioritize patient needs and deliver timely‚ effective care.

2.2 Improved Accuracy in Documentation

Printable nursing report sheets enhance documentation accuracy by providing structured sections for patient information‚ medications‚ and vital signs. Checkboxes and pre-designed fields reduce errors and ensure consistency. These templates prevent omissions by guiding nurses through essential details‚ fostering precise and reliable documentation. The organized format minimizes misunderstandings‚ ensuring accurate handoffs and continuity of care‚ which is critical for patient safety and effective treatment plans.

2.3 Consistency in Reporting Across Healthcare Settings

Printable nursing report sheets ensure consistency in documentation across various healthcare settings‚ from hospitals to nursing homes. Standardized templates provide uniformity in recording patient details‚ medications‚ and vital signs‚ reducing confusion during handoffs. This consistency enables healthcare providers to quickly understand patient information‚ regardless of the facility‚ fostering clear communication and continuity of care. It also aids in maintaining uniformity in reporting standards‚ enhancing overall patient outcomes and collaboration among healthcare teams.

Types of Nursing Report Sheet Templates

Printable nursing report sheet templates come in various formats‚ including SBAR‚ Brain sheets‚ and customizable designs. These templates cater to different healthcare settings and specific needs.

3.1 SBAR (Situation‚ Background‚ Assessment‚ Recommendation) Format

The SBAR format is a widely used framework in nursing report sheets‚ offering a structured approach to communication. It includes sections for Situation‚ Background‚ Assessment‚ and Recommendation‚ ensuring clear and concise reporting. This method is particularly effective in high-stakes environments like hospitals and emergency care‚ promoting accurate and timely information exchange among healthcare professionals. Its organized layout enhances readability and prioritizes patient safety.

3.2 Brain Sheet Format for Nursing Reports

The Brain Sheet format is a popular nursing report template designed to organize patient information efficiently. It typically includes sections for patient details‚ medications‚ vital signs‚ and care plans‚ allowing nurses to quickly access critical data. This format is structured yet flexible‚ accommodating various clinical scenarios. Its simplicity and focus on essential information make it ideal for fast-paced environments like ICUs or emergency departments‚ ensuring accurate and timely documentation.

3.3 Customizable Templates for Specific Needs

Customizable nursing report sheet templates offer flexibility‚ allowing users to tailor sections‚ fonts‚ and colors to meet specific clinical requirements. Available in formats like PDF‚ PNG‚ and JPG‚ these templates can be adapted for various healthcare settings‚ including hospitals‚ clinics‚ and home care; Their adjustability ensures they cater to diverse patient needs‚ making them versatile tools for organized and efficient documentation across different medical environments and patient scenarios.

How to Create a Nursing Report Sheet Template

Design a template by including sections for patient info‚ medications‚ and vital signs. Ensure a clear layout for readability and save as PDF or editable formats.

4.1 Step-by-Step Guide to Designing a Template

To create a nursing report sheet‚ start by defining its purpose and identifying necessary sections. Add a title and patient information fields. Include sections for vital signs‚ medications‚ and care plans; Use tables or checkboxes for clarity. Save the template in PDF or editable formats for flexibility. Ensure the design is user-friendly and adaptable to different healthcare settings for optimal efficiency.

4.2 Key Elements to Include in a Nursing Report Sheet

A nursing report sheet should include patient demographics‚ vital signs‚ medications‚ assessments‚ and care plans. Add sections for progress notes and clinical investigations. Use checkboxes and tables for quick documentation. Ensure readability with clear headings and spacing. Customize the template to meet specific healthcare needs‚ such as SBAR or brain sheet formats. Include date and time fields for accurate tracking and accountability.

Downloading and Printing Nursing Report Sheets

Printable nursing report sheets are readily available online in PDF format‚ allowing easy downloading and printing. Templates are designed for clarity and efficiency in healthcare settings.

5.1 Availability of Free Printable Templates Online

Free printable nursing report sheet templates are widely available online in PDF format‚ offering convenience for healthcare professionals. Websites like NRSNG.com provide downloadable templates‚ including SBAR and brain sheet formats‚ suitable for various clinical settings; These templates are easily accessible‚ customizable‚ and designed to streamline patient documentation‚ making them invaluable tools for nurses seeking organized and efficient reporting solutions.

Available in PDF for easy printing
Customizable to meet specific needs
Suitable for multiple healthcare settings

5.2 Steps to Download and Print Nursing Report Sheets

Downloading and printing nursing report sheets is straightforward. Visit websites offering free templates‚ select the desired format‚ and click the download button. Ensure your printer is set to the correct paper size‚ such as A4 or US Letter. Print the template on standard paper for easy use during shifts. Many templates are available in PDF format for quick access and printing convenience.

Choose a template from a reliable source
Download the template in PDF format
Adjust printer settings for optimal output
Print on standard paper for practical use

Features of a Good Nursing Report Sheet

A good nursing report sheet includes sections for patient details‚ medications‚ vital signs‚ and assessments. It offers formatting options like colors and layouts for better readability and organization.

Patient information section
Medication list
Vital signs chart
Assessment notes

6.1 Sections and Layout for Organized Documentation

A well-designed nursing report sheet includes sections for patient demographics‚ medications‚ vital signs‚ and assessments‚ ensuring all critical information is captured systematically. The layout is structured to enhance readability‚ with clear headings and organized fields‚ making it easy for nurses to document and retrieve patient data efficiently during busy shifts.

Patient information section
Medication list
Vital signs chart
Assessment notes

6.2 Formatting Options for Better Readability

Printable nursing report sheets often include adjustable font sizes‚ high-contrast colors‚ and spaced sections to improve readability. These formatting options ensure that critical patient information is easy to scan‚ reducing errors and saving time during busy shifts. Customizable templates also allow nurses to tailor the layout to their specific needs‚ enhancing clarity and efficiency in documenting patient care.

Adjustable font sizes
High-contrast colors
Proper spacing between sections

Use Cases for Nursing Report Sheets

Printable nursing report sheets are widely used in hospitals‚ clinics‚ nursing homes‚ and home healthcare settings to ensure organized and efficient patient care documentation.

7.1 Hospitals and Clinics

Printable nursing report sheets are invaluable in hospitals and clinics‚ where organized patient data is critical. They help nurses manage multiple patients‚ track progress‚ and ensure continuity of care. These templates are especially useful in high-pressure environments‚ allowing for quick documentation of vital signs‚ medications‚ and assessments. Their structured format‚ including sections for patient demographics and treatment plans‚ supports efficient communication and reduces errors‚ making them indispensable in fast-paced clinical settings.

7.2 Nursing Homes and Long-Term Care Facilities

Printable nursing report sheets are tailored for long-term care‚ aiding nurses in documenting residents’ ongoing conditions‚ medications‚ and daily progress. These templates‚ often in PDF format‚ provide a clear structure for tracking vital signs‚ dietary needs‚ and therapy updates‚ ensuring comprehensive care plans. Their portability and customization make them ideal for facilities requiring detailed‚ consistent records‚ enhancing resident care and simplifying report sharing among staff.

7.3 Home Healthcare Settings

Printable nursing report sheets are ideal for home healthcare‚ offering a portable solution for documenting patient care in non-clinical environments. These PDF templates allow nurses to record vital signs‚ treatment plans‚ and patient progress efficiently. Their structured format ensures consistency‚ even in remote settings‚ facilitating seamless communication between healthcare providers and improving continuity of care for patients receiving treatment at home.

Tips for Effective Use of Nursing Report Sheets

Use printable nursing report sheets to stay organized‚ ensuring accuracy and efficiency. Customize templates to fit specific needs‚ and review regularly to maintain clarity and comprehensiveness in documentation.

8.1 Best Practices for Filling Out Report Sheets

Start each shift by initiating a new report sheet‚ ensuring all patient information‚ medications‚ and vital signs are clearly documented. Organize data in designated sections for readability. Prioritize concise and accurate entries to avoid errors. Review the sheet before handing off to ensure continuity of care. Regular updates and legible handwriting are crucial for effective communication among healthcare team members.

8.2 Time Management Strategies for Busy Nurses

Optimize your workflow by using printable nursing report sheets to streamline documentation. Prioritize tasks‚ focusing on critical patient data first. Use pre-designed templates to save time during busy shifts. Ensure all sections are filled succinctly and legibly‚ reducing delays. Regularly review and update the report sheet to maintain accuracy and efficiency‚ allowing for seamless communication during handoffs and minimizing time spent on repetitive tasks.

Printable nursing report sheets are invaluable tools‚ enhancing organization‚ efficiency‚ and patient care quality. Their structured format ensures consistency‚ aiding nurses in delivering precise and timely documentation across healthcare settings.

9.1 Summary of Key Points

Printable nursing report sheets are vital tools for organizing patient data‚ ensuring efficient communication‚ and maintaining accurate documentation. They offer customizable templates‚ including SBAR and brain sheet formats‚ tailored to specific healthcare settings. These sheets are widely available in formats like PDF‚ making them accessible for hospitals‚ clinics‚ and home care. Their structured design enhances clarity‚ reducing errors and improving patient care outcomes significantly.

9.2 Final Thoughts on the Value of Printable Nursing Report Sheets

Printable nursing report sheets are indispensable tools for modern healthcare‚ offering organized‚ efficient‚ and clear documentation. Their versatility‚ customization options‚ and accessibility in formats like PDF make them invaluable for nurses across various settings. By streamlining communication and reducing errors‚ these sheets enhance patient care quality‚ proving their essential role in healthcare professionals’ daily workflows and long-term patient management strategies.

Bybeatrice

interqual criteria manual 2023 pdf

The InterQual Criteria Manual 2023 PDF provides evidence-based guidelines for clinical decision-making, focusing on patient severity, comorbidities, and care continuum needs, updated for 2023 standards.

Overview of the InterQual Criteria Manual

The InterQual Criteria Manual 2023 is a comprehensive resource designed to guide clinical decision-making across the continuum of care. It provides evidence-based criteria to assess patient severity of illness, comorbidities, and care needs. The manual is structured in a decision-tree format, enabling healthcare professionals to navigate complex clinical scenarios efficiently. It covers various care settings, including acute care, ambulatory care, and post-acute care, ensuring consistent and standardized evaluations. The criteria are updated annually to reflect the latest clinical advancements and regulatory requirements. This tool is widely used by payers, providers, and utilization review teams to ensure appropriate resource allocation and optimal patient outcomes. Its clear, objective guidelines help reduce variability in clinical decisions, promoting transparency and accountability in healthcare delivery. The InterQual Criteria Manual 2023 is a vital resource for ensuring high-quality, patient-centered care.

Importance of the 2023 Edition

The 2023 edition of the InterQual Criteria Manual holds significant importance due to its updated clinical guidelines and enhanced decision-making tools. It incorporates the latest medical advancements, ensuring that healthcare providers have access to current, evidence-based standards. This edition particularly emphasizes updates in acute adult level of care and hematology/oncology subsets, reflecting evolving patient needs and treatment protocols. The revisions aim to improve care quality, patient safety, and resource utilization. By aligning with the 2023 updates, healthcare organizations can maintain compliance with regulatory changes and payer requirements. Additionally, the enhanced criteria support more accurate and efficient clinical reviews, reducing administrative burdens. This makes the 2023 edition indispensable for professionals seeking to deliver high-quality, cost-effective care while adhering to contemporary medical practices;

Key Features of the InterQual Criteria Manual 2023

The 2023 InterQual Criteria Manual features a decision-tree format, updated clinical guidelines, and expanded coverage of the care continuum, including hematology/oncology and ambulatory care subsets.

Updates and Revisions in the 2023 Edition

The 2023 InterQual Criteria Manual includes significant updates, such as revised Acute Adult Level of Care guidelines and streamlined Hematology/Oncology subsets, now condensed into two categories. Ambulatory Care Planning Criteria have been enhanced for better clinical decision-making. Effective May 1, 2023, these changes ensure alignment with current medical practices, improving care quality and efficiency. The manual also introduces updated decision-tree formats for clearer navigation and objective endpoints for service reviews. These revisions reflect the latest clinical evidence and aim to reduce administrative burdens while enhancing payer-provider collaboration. The updates are part of ongoing efforts to refine care continuum assessments, ensuring accurate and patient-specific evaluations across various care settings.

Decision-Tree Format for Clinical Decision-Making

The 2023 InterQual Criteria Manual employs a decision-tree format to streamline clinical decision-making. This structured approach presents criteria in a logical flow, enabling users to assess patient needs systematically. The decision-tree format simplifies complex clinical scenarios by breaking them into sequential steps, ensuring clarity and consistency. It guides reviewers through evaluating patient severity, comorbidities, and treatment requirements, ultimately determining the appropriate level of care. This intuitive design enhances efficiency, reducing the time spent on reviews while maintaining accuracy. The format is particularly useful for objective endpoints in service reviews, such as inpatient rehabilitation and skilled nursing care. By organizing criteria in this manner, the manual supports defensible and patient-specific decisions, aligning with current clinical practices and standards.

Coverage of Continuum of Care

The InterQual Criteria Manual 2023 PDF provides comprehensive coverage of the continuum of care, addressing various clinical settings and patient needs. It includes detailed criteria for inpatient rehabilitation, subacute care, and skilled nursing facilities, ensuring seamless transitions between care levels. The manual incorporates objective endpoints for service reviews, enabling accurate assessments of patient severity and treatment requirements. This holistic approach supports healthcare providers in making informed decisions tailored to individual patient needs. The 2023 edition also includes updates to specific care subsets, such as Hematology/Oncology, enhancing the manual’s relevance to modern clinical practices. By addressing the full spectrum of care, the InterQual Criteria Manual serves as a valuable resource for ensuring appropriate and effective patient management across all care settings, aligning with current clinical standards and guidelines; This ensures continuity and consistency in patient care delivery.

Accessing the InterQual Criteria Manual 2023 PDF

Accessing the InterQual Criteria Manual 2023 PDF requires logging into the Change Healthcare platform. Users must navigate to the Quick Access section to download the updated manual.

Steps to Download the InterQual Criteria Manual

To download the InterQual Criteria Manual 2023 PDF, users must first log in to the Change Healthcare InterQual platform using their credentials. Once logged in, navigate to the Quick Access section, typically located at the bottom left of the homepage. From there, select the appropriate option to access the InterQual Criteria Manual 2023. Follow the prompts to download the PDF version of the manual. Ensure your account has the necessary permissions to access the document. The platform may also provide additional resources or updates alongside the manual. Downloading the manual ensures access to the latest clinical guidelines and decision-making tools, supporting efficient and informed patient care decisions. This process is streamlined to facilitate quick and secure access to the updated 2023 criteria.

Platform Navigation and Login Requirements

Accessing the InterQual Criteria Manual 2023 PDF requires logging in to the Change Healthcare InterQual platform. Users must have valid credentials, typically provided by their organization or purchased directly. Once logged in, navigate to the platform’s homepage and locate the Quick Access section, usually found at the bottom left. From there, select the option to view or download the InterQual Criteria Manual 2023. The platform may also require additional steps, such as verifying user permissions or selecting specific modules. The interface is designed to streamline navigation, with clear menus and search functions to locate the manual efficiently. Ensure your browser and software are up to date for optimal performance. If issues arise, refer to the platform’s help resources or contact support for assistance.

Clinical Applications of the InterQual Criteria

The InterQual Criteria supports clinical decision-making across various settings, including acute adult care, hematology/oncology, and ambulatory care, ensuring appropriate patient management and resource allocation.

Acute Adult Level of Care Updates

The 2023 InterQual Criteria Manual includes significant updates to the Acute Adult Level of Care guidelines, focusing on enhanced clinical decision-making. These updates reflect advancements in patient care and evidence-based practices. Key revisions include streamlined criteria for assessing patient severity of illness, comorbidities, and complications. The 2023 edition also introduces refined thresholds for determining appropriate levels of care, ensuring alignment with current clinical standards. Providers can expect clearer guidelines for acute care settings, facilitating more accurate and efficient patient assessments. These updates aim to improve resource allocation and ensure patients receive the most appropriate level of care based on their clinical needs. Effective dates for these changes vary by provider, with many transitioning to the 2023 criteria starting in early 2023. This ensures continuity in care and adherence to the latest clinical recommendations.

Hematology/Oncology Subsets

The 2023 InterQual Criteria Manual features updated Hematology/Oncology subsets, designed to enhance clinical decision-making in oncology care. A key change includes the consolidation of six previous subsets into two streamlined categories, improving clarity and reducing redundancy. These updates ensure more precise assessments for patients with complex hematologic and oncologic conditions. The revised criteria incorporate current treatment protocols and evidence-based guidelines, reflecting advancements in oncology care. This restructuring helps providers make more accurate determinations regarding appropriate levels of care for patients with conditions such as leukemia, lymphoma, and other hematologic malignancies. The 2023 edition also emphasizes the importance of patient-specific factors, such as disease progression and treatment response, in care planning. These updates aim to support optimal outcomes while aligning with contemporary clinical practices in hematology and oncology.

Ambulatory Care Planning Criteria

The InterQual Criteria Manual 2023 PDF includes comprehensive Ambulatory Care Planning Criteria, designed to support efficient and evidence-based decision-making in outpatient settings. These criteria are presented in an intuitive question-and-answer (Q&A) format, ensuring clarity and ease of use for healthcare providers. The updated 2023 edition incorporates extensive informational notes and references, providing guidance for clinical recommendations and enhancing workflow efficiency. The ambulatory care criteria address a wide range of services, including adult and pediatric procedures, durable medical equipment, and imaging procedures. By leveraging evidence-based guidelines, the InterQual system helps reviewers assess the appropriateness of care and ensure optimal patient outcomes in ambulatory settings. This feature is particularly valuable for providers navigating complex clinical scenarios, as it offers a structured approach to care planning and resource allocation. The 2023 updates further refine these criteria to align with contemporary clinical practices and standards.

The InterQual Criteria Manual 2023 PDF serves as a pivotal resource for healthcare professionals, offering evidence-based guidelines to enhance clinical decision-making and patient care. With its comprehensive updates, the 2023 edition ensures alignment with contemporary medical practices, providing clear and structured criteria for various care settings. The decision-tree format and detailed clinical references simplify complex reviews, enabling efficient and accurate assessments. By addressing the continuum of care and incorporating updates in specialized areas like hematology/oncology, the manual supports providers in delivering high-quality, patient-centered care. Its emphasis on evidence-based practices and intuitive design makes it an indispensable tool for improving care quality and operational efficiency across healthcare organizations. This resource continues to play a critical role in advancing clinical excellence and ensuring optimal patient outcomes.

Bybeatrice

cuento de masha y el oso pdf

Introducing Masha, a curious girl, and her guardian, a gentle Bear, in a timeless Russian folktale․ Their forest adventures highlight friendship, kindness, and growth, captivating audiences globally․ Available in an adapted PDF with pictograms, this story remains a beloved classic․

1․1 Overview of the Tale

Masha, a curious and energetic girl, ventures into the forest, where she encounters a gentle Bear․ Their adventures explore themes of friendship, responsibility, and growth․ The story, rooted in Russian folklore, has been adapted into various formats, including a popular PDF version with pictograms, making it accessible to children worldwide․ This adaptation simplifies the narrative, using visual aids to enhance understanding and engagement․ The tale’s universal appeal lies in its timeless lessons and the charming dynamic between Masha and the Bear, fostering both entertainment and moral growth for young audiences․

1․2 Main Characters: Masha and the Bear

Masha is a lively, curious girl who loves exploration and play․ Her adventurous spirit often leads her into mischief, making her a relatable and endearing character to children․ The Bear, her guardian, is a kind, protective figure who balances firmness with affection․ Despite his occasional sternness, he cares deeply for Masha, teaching her valuable life lessons․ Their contrasting personalities create a dynamic that captivates young audiences, emphasizing themes of friendship, responsibility, and growth․ Together, they form the heart of the story, making their adventures both entertaining and educational․

Origin and Cultural Significance

A traditional Russian folktale, “Masha and the Bear” reflects cultural values and simplicity, passed down through generations․ Its adaptation with pictograms enhances accessibility, blending tradition with modern learning tools․

2․1 Traditional Russian Folk Tale

Masha and the Bear is a cherished Russian folktale that has been passed down through generations․ The story revolves around a curious girl named Masha who ventures into the forest, encountering a bear․ The narrative highlights themes of kindness, responsibility, and growth․ Originating from traditional Russian folklore, it reflects simple yet profound life lessons․ The tale has been shared orally before being adapted into various formats, including animated series and illustrated books․ Its enduring popularity stems from its universal appeal and the timeless moral values it conveys, making it a cultural gem in Russian heritage․

2․2 Adaptation with Pictograms for Better Understanding

The story of Masha and the Bear has been adapted with pictograms to enhance comprehension, especially for children and individuals with cognitive or learning needs․ These visual aids simplify complex scenes, making the narrative more accessible․ The adaptation retains the original moral lessons while adding a layer of engagement through imagery․ Pictograms help readers connect words with actions, fostering a deeper understanding of the story․ This version is particularly beneficial for early learners or those requiring additional support, ensuring the tale’s universal appeal endures across diverse audiences․

Plot Summary

Masha, a curious girl, gets lost in the forest and meets a protective bear․ Their adventures teach mutual respect and responsibility through their shared experiences, fostering a lasting bond․

3․1 Masha’s Adventure in the Forest

Masha, a curious and adventurous girl, ventures into the forest to gather berries and mushrooms․ While exploring, she stumbles upon the Bear’s cozy cabin, unaware of the chaos she is about to create․ Her playful nature leads her to rearrange the Bear’s belongings, breaking his fishing rod and causing disorder․ As she enjoys her newfound playhouse, the Bear returns, discovering the mess․ Masha’s journey reflects her spontaneity and innocence, setting the stage for a transformative encounter with the Bear․

3․2 The Bear’s Reaction and Lesson Learned

The Bear, tired from his outing, returns to find his cabin in disarray․ Masha’s playful chaos angers him, and he scolds her, taking her deep into the forest․ Left alone in the dark, Masha realizes her actions’ consequences․ The Bear, reflecting on his harshness, later softens, recognizing Masha’s innocence․ This encounter teaches Masha about responsibility, while the Bear learns patience, fostering mutual understanding and respect in their unique friendship․ The story beautifully balances discipline with compassion, offering a timeless moral lesson for young readers․

Educational Value

The story enhances cognitive and emotional development in children; Visual aids like pictograms make the narrative engaging, fostering understanding and sparking imagination in young minds effectively․

4․1 Cognitive and Emotional Development

The story of Masha and the Bear fosters cognitive growth by enhancing memory and problem-solving skills through engaging narratives․ The use of pictograms aids visual learning, making complex ideas accessible․ Emotionally, it teaches children to recognize and manage feelings, understand consequences of actions, and develop empathy․ Masha’s curiosity and resilience inspire creativity, while the Bear’s patience models kindness and responsibility․ This blend of adventure and moral lessons creates a nurturing environment for holistic child development, making the story a valuable educational tool for young learners worldwide․

4․2 Use of Visual Aids like Pictograms

The adaptation of “Masha and the Bear” with pictograms enhances storytelling by providing visual cues․ These symbols simplify complex narratives, aiding comprehension for young readers and those with learning challenges․ By breaking down the story into visual elements, pictograms make the tale more accessible and engaging․ They also support language development, allowing children to connect words with images․ This visual approach fosters a deeper understanding of the plot and characters, making the story more interactive and enjoyable for learners of all ages and abilities․

Downloading the PDF Version

The PDF version of “Masha and the Bear” is easily accessible online․ Sources like Orientación Andujar offer free downloads, allowing readers to enjoy the story anytime, anywhere․

5․1 Sources for the PDF

The PDF version of “Masha and the Bear” can be downloaded from various trusted sources․ Platforms like Orientación Andujar and Archive․org provide free access to the adapted story with pictograms․ These sources ensure the story is accessible to children and educators worldwide․ Additionally, websites like jardininfantilrukantu․cl and Scribd offer downloadable versions, making it easy to share and enjoy․ The PDF format allows for offline reading, ensuring the tale of Masha and the Bear remains a convenient and engaging resource for all audiences․

5․2 Steps to Access the Adapted Story

To access the adapted story in PDF format, visit trusted platforms like Orientación Andujar or Archive․org․ Search for “Masha and the Bear” or “Cuento de Masha y el Oso” on these sites․ Select the desired version and follow the download instructions․ Some platforms may require free registration․ Once downloaded, the PDF can be saved for offline reading․ Ensure to verify the source’s reliability for a safe and smooth download experience․ This convenient process makes the story accessible to children and educators worldwide․

Popular Adaptations

Masha and the Bear has been adapted into a globally popular TV series, movies, and special episodes, entertaining audiences while staying true to the original folktale’s charm․

6․1 The TV Series Phenomenon

The animated TV series Masha and the Bear has become a global phenomenon, captivating millions of viewers worldwide․ Produced by Animaccord, the series first aired in 2009 and has since grown into a beloved franchise․ It follows the adventures of Masha, a spirited young girl, and her guardian, a gentle bear, as they explore the forest and learn valuable lessons․ The show’s blend of humor, kindness, and moral teachings has made it a favorite among children and parents alike․ Its availability on platforms like YouTube has further boosted its popularity, making it a modern classic in children’s entertainment․

6․2 Movies and Special Episodes

Building on the success of the TV series, Masha and the Bear has expanded into movies and special episodes․ The full-length film, Masha and the Bear: The Movie, offers exciting adventures beyond the usual episodes․ Special episodes, such as Christmas-themed stories, bring festive joy and unique storylines․ These productions maintain the core values of friendship and learning while introducing new characters and challenges․ The movies and specials have become a delightful addition to the franchise, further enchanting fans worldwide with their charm and creativity․

Why It’s Beloved Worldwide

Masha and the Bear captivates audiences globally with its blend of entertainment and moral lessons․ Its universal themes, paired with visually engaging adaptations, make it a cherished tale worldwide․

7․1 Universal Appeal to Children

Masha and the Bear captivates young audiences worldwide with its vibrant animation, relatable characters, and engaging storylines․ Masha’s curiosity and the Bear’s kindness create a dynamic duo that resonates with children’s natural sense of wonder․ The tales are filled with humor, adventure, and heartfelt moments, making them accessible to diverse cultures․ The use of pictograms in adapted versions further enhances comprehension, allowing children to follow the narrative visually․ This timeless story fosters emotional and cognitive growth while entertaining, making it a global favorite among kids and parents alike․

7․2 Moral Lessons and Entertainment

Masha and the Bear seamlessly blends entertainment with moral lessons, making it a delightful yet educational experience for children․ Masha’s curiosity often leads to mischief, while the Bear’s patience teaches her valuable life lessons․ The stories emphasize kindness, responsibility, and understanding consequences, all while maintaining a lighthearted tone․ This balance of fun and learning makes the tale engaging for young audiences, helping them develop essential values in an enjoyable way․ The moral depth, combined with its entertaining narrative, ensures the story’s enduring popularity across generations․

The tale’s enduring charm lies in its blend of entertainment and education, offering universal lessons that captivate global audiences while fostering children’s growth․

8․1 Final Thoughts on the Story’s Impact

Masha and the Bear’s enduring appeal lies in its universal themes of friendship and growth, making it a cherished tale worldwide․ The story’s cultural roots and its adaptation with pictograms have broadened its accessibility, especially for children with special needs․ Its perfect blend of entertainment and education ensures it remains a timeless classic, fostering emotional and cognitive development in young minds․ As a result, Masha and the Bear continues to captivate audiences, leaving a lasting legacy in children’s literature and education․

Master Every Task with Clear Guidelines

Category Archive PDF

parent functions chart pdf

1.1 Definition and Importance of Parent Functions

1;2 Overview of the Parent Functions Chart

Types of Parent Functions

2.1 Linear Functions

2.2 Nonlinear Functions (Quadratic, Cubic, etc.)

2.3 Absolute Value and Piecewise Functions

2.4 Root and Rational Functions

Graphical Transformations of Parent Functions

3.1 Vertical and Horizontal Shifts

3.2 Stretching and Compressing (Scaling)

3.3 Reflections Over the x-axis or y-axis

3.4 Combining Multiple Transformations

Attributes of Parent Functions

4.1 Domain and Range

4.2 End Behavior and Symmetry

4.3 Increasing or Decreasing Intervals

Using the Parent Functions Chart

5.1 Identifying Basic Functions

5.2 Analyzing Transformations

5.3 Sketching Graphs

Examples and Applications

6.1 Real-World Applications of Parent Functions

6.2 Solving Problems with Transformations

Educational Resources

7.1 PDF Guides and Worksheets

7.2 Online Tools and Tutorials

Best Practices for Learning Parent Functions

8.1 Structured Study Techniques

8.2 Common Mistakes to Avoid

thank you maam pdf

Plot Summary

Setting

The Incident

Major Characters

Mrs․ Luella Bates Washington Jones

Roger

Themes

Kindness and Redemption

Social and Economic Factors

Symbolism

The Purse

The Blue Suede Shoes

Analysis

Author’s Message

Critical Reception

krapp’s last tape pdf

1.1 Overview of the Play

1.2 Historical Context and Background

Plot Summary of “Krapp’s Last Tape”

2.1 The Setting: Krapp’s Den

2.2 The Narrative Structure: Past and Present

Themes in “Krapp’s Last Tape”

3.1 Memory and Regret

3.2 The Passage of Time and Mortality

3.3 Loneliness and Isolation

Character Analysis: Krapp

4.1 Psychological Profile of Krapp

4.2 Krapp’s Relationship with His Past Self

Dramatic Structure and Style

5.1 The Use of Monologue

5.2 The Role of the Tape Recorder

Symbolism in the Play

6.1 The Significance of the Tape Recorder

6.2 The Symbolism of Krapp’s Den

Reception and Impact

7.1 Critical Responses to the Play

7.2 Influence on Modern Theater

Notable Productions and Adaptations

8.1 Landmark Productions Featuring Stephen Rea

8.2 Gary Oldman’s Interpretation of Krapp

Educational Resources and Further Reading

9.1 Availability of “Krapp’s Last Tape” in PDF Format

9.2 Recommended Secondary Sources and Analyses

10.1 Summary of Key Themes and Ideas

geopolitics: making sense of a changing world pdf

Understanding Geopolitics: An Overview

Defining Geopolitics